Fizyka – wybrane zagadnienia

Zw względu na fakt, że we wcześniejszych fragmentach tej strony znajdują się zagadnienia dotyczące mechaniki kwantowej, to zrozumiałym wydaje się omówienie wybranych zagadnień z zakresu fizyki.

Zapoznanie się z podstawowymi pojęciami mechaniki i elektrodynamiki w ujęciu klasycznym umożliwi zrozumienie, nie zawsze intuicyjnych, pojęć mechaniki kwantowej, a ponadto pozwoli na dostrzeżenie różnic opisu rzeczywistości na gruncie tych dwóch teorii. Takie pojęcia jak pęd czy hamiltonian, odgrywające podstawową rolę w mechanice kwantowej, są oczywiście składnikami mechaniki klasycznej i należy mieć świadomość jaką interpretację fizyczną posiadają na gruncie tej teorii.

Równania ruchu

Podstawowym pojęciem mechaniki jest pojęcie punktu materialnego, czy też cząstki. Definiuje ono ciało materialne, którego rozmiary można pominąć przy opisie jego ruchu. Położenie punktu materialnego w przestrzeni jest określane przez jego wektor wodzący r, którego składowe są współrzędnymi kartezjańskimi x, y , z. Pochodna wektora r względem czasu dr/dt = v nazywa się prędkością. Natomiast druga pochodna d²r/dt² jest przyspieszeniem punktu materialnego. Różniczkowanie względem czasu często oznacza się przy pomocy kropki nad danym symbolem, czyli v = ṙ.

Położenie N punktów materialnych określa się za pomocą N wektorów wodzących czyli 3N współrzędnych. Liczba niezależnych wielkości, których znajomość jest konieczna do opisu układu nosi nazwę liczby stopni swobody układu. W tym przykładzie liczba stopni swobody wynosi 3N, ale nie muszą to być w ogólności współrzędne kartezjańskie punktów. W zależności od warunków zagadnienia jakie rozpatrujemy wygodniejszy niż współrzędne kartezjańskie może być wybór dowolnych wielkości q_s, charakteryzujących układ o s stopniach swobody. Wielkości te noszą nazwę współrzędnych uogólnionych, a ich pochodne względem czasu są prędkościami uogólnionymi. Jednoczesna znajomość wszystkich współrzędnych i prędkości całkowicie określa stan układu i pozwala na przewidzenie jego ruchu. Z matematycznego punktu widzenia oznacza to, że znajomość współrzędnych i prędkości wszystkich elementów układu w pewnej chwili czasu jednoznacznie określa przyspieszenie w danej chwili. Związki łączące przyspieszenie ze współrzędnymi i prędkościami noszą nazwę równań ruchu. Ponieważ są to równania różniczkowe drugiego rzędu na funkcje q(t) to ruch układu mechanicznego można określić w wyniku całkowania tych równań.

Najbardziej ogólnym sformułowanie praw ruchu jest zasada najmniejszego działania, zwana tez zasadą Hamiltona. W myśl tej zasady każdy układ mechaniczny jest charakteryzowany przez pewną funkcję jego współrzędnych, prędkości i czasu, a ruch tego układu spełnia pewien warunek. Dla określenia tego warunku rozpatrzmy układ, który w pewnych chwilach czasu t₁ i t₂ ma określone położenia charakteryzowane przez zbiory wartości współrzędnych. Pomiędzy tymi położeniami układ porusza się tak, że całka:

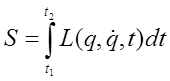przyjmuje najmniejszą możliwą wartość. Funkcję L nazywa się funkcją Lagrange’a danego układu, a całka S jest działaniem układu. W celu znalezienia równań różniczkowych, których rozwiązania będą minimalizować całkę S załóżmy, że układ ma tylko jeden stopień swobody. W takim wypadku szukamy tylko jednej funkcji q = q(t). Jeżeli dla tej funkcji całka S ma minimum to jasnym jest, że S będzie wzrastało jeżeli zastąpimy q(t) dowolną funkcją postaci q(t) + δq(t) gdzie δq(t) jest funkcją małą w całym przedziale od t₁do t₂. Funkcję δq(t) nazywa się wariają funkcji q(t). Ponieważ dla czasów t₁ i t₂. wszystkie funkcje  powinny przyjmować wartości q₁ i q₂ to wariacja powinna spełniać warunek:

δq(t₁) = δq(t₂) = 0.

Zastąpienie q przez q + δq zmienia działanie w sposób określony przez różnicę:

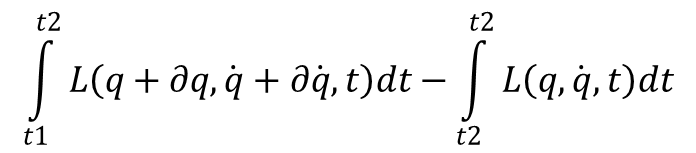Teraz aby działanie przyjmowało minimum koniecznym jest żeby wariacja całki S była równa zero, czyli

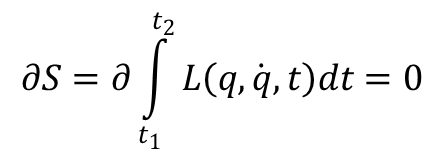lub rozpisując to wyrażenie zgodnie z definicją wariacji:

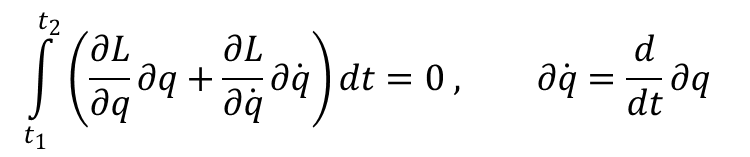Całkując drugi wyraz przez części otrzymujemy:

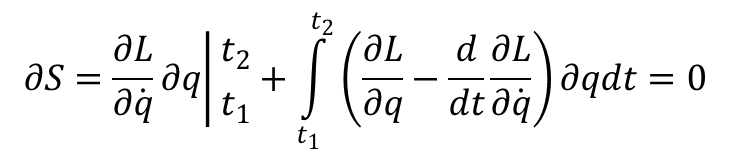W tym wyrażeniu na mocy warunku δq(t₁) = δq(t₂) = 0 znika pierwszy wyraz, a druga całka powinna znikać przy dowolnych wartościach wariacji δq. Jest to możliwe tylko gdy wyrażenie podcałkowe jest równe zero, czyli:

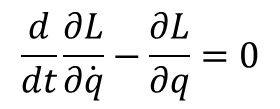Jeżeli układ ma więcej stopni swobody to równanie przybiera postać:

Równania te noszą nazwę równań Lagrange’a, a jeżeli znana jest funkcja Lagrange’a układu mechanicznego określają one związki pomiędzy przyspieszeniami, prędkościami i współrzędnymi, a tym samym są one równaniami ruchu układu. Z matematycznego punktu widzenia jest to układ n-równań różniczkowych drugiego rzędu dla n niewiadomych funkcji q_i(t). Ogólne rozwiązanie takiego układu zależy od 2n dowolnych stałych. Dla określenia tych stałych, a tym samym całkowitego ruchu układu, należy znać warunki początkowe charakteryzujące układ w pewnej chwili czasu. Weźmy pod uwagę układ składający się z dwóch niezależnych części A i B, które charakteryzują dwie funkcje Lagrange’a L_A i L_B. Odsuwając od siebie obydwie części układu, tak aby w granicy zaniedbać ich wzajemne oddziaływanie funkcja Lagrange’a całego układu dąży do:

limL = L_A+ L_B

Addytywność funkcji Lagrange’a jest równoważna stwierdzeniu, że ruch każdej nieoddziałującej części układu nie może zawierać wielkości odnoszących się do części pozostałych. Oczywiście pomnożenie funkcji L układu mechanicznego przez dowolną stała nie ma wpływu na równania ruchu. Takie stwierdzenie prowadzi do nieokreśloności polegającej na tym, że funkcje Lagrange’a różnych odosobnionych układów mechanicznych można mnożyć przez dowolne różne stałe. Własność addytywności usuwa tę nieokreśloność pozostawiając jedynie możliwość mnożenia funkcji Lagrange’a wszystkich części układu przez jednakową stała, co sprowadza się do dowolności wyboru jednostek wymiarów wielkości fizycznych. Dodatkowo dwie funkcje Lagrange’a różniące się tylko zupełną pochodną czasową dowolnej funkcji współrzędnych i czasu prowadzą do tych samych równań ruchu. To wskazuje, że funkcja Lagrange’a jest określona tylko z dokładnością do addytywnej funkcji, będącej zupełną pochodną dowolnej funkcji współrzędnych i czasu.

Układ odniesienia

Do opisu zjawisk zachodzących w przyrodzie należy wybrać pewien układ odniesienia, czyli układ współrzędnych, w którym określamy położenia cząstek w przestrzeni oraz związane z tym układem zegary względem których określamy czas. Najprostszy rodzaj ruchu to ruch ciała swobodnego, czyli takiego, które nie podlega oddziaływaniom zewnętrznym. Istnieją układy odniesienia, w których ruch swobodny odbywa się ze stałą co do wielkości i kierunku prędkością. Układy takie nazywa się układami inercjalnymi. Własność inercjalności można sformułować w oparciu o stwierdzenie o jednorodności i izotropii przestrzeni oraz o jednorodności czasu względem takiego układu odniesienia. Jednorodność przestrzeni i czasu oznacza równoważność wszystkich położeń cząstki w przestrzeni i wszystkich momentów czasu. Natomiast izotropia przestrzeni jest związana z równoważnością wszystkich kierunków w przestrzeni. Ponieważ jeżeli jeden układ odniesienia porusza się względem drugiego ruchem jednostajnym prostoliniowym i jeżeli jeden z tych układów jest inercjalny to i drugi musi być inercjalny. To wskazuje, że istnieje dowolnie dużo układów inercjalnych, w których ruch swobodny odbywa się z ze stałą prędkością. Istotne jest to, że we wszystkich różnych układach inercjalnych wszystkie prawa przyrody są jednakowe. Jest to treść zasady względności, zgodnie z którą równania wyrażające prawa przyrody są niezmiennicze ze względu na przekształcenia współrzędnych i czasu, spowodowane przejściem z jednego układu inercjalnego do innego. Obok zasady względności, na gruncie mechaniki klasycznej, obowiązuje założenie o czasie bezwzględnym, czyli o jednakowym przebiegu czasu we wszystkich układach inercjalnych. Połączenie tych dwóch zasad stanowi treść zasady względności Galileusza.

Współrzędne r i r’ tego samego punktu w dwóch różnych układach inercjalnych, z których jeden porusza się z prędkością V względem drugiego są związane zależnością:

r = r’ + Vt

gdzie t jest czasem jednakowym w obydwu układach. Różniczkując obie strony równania po czasie otrzymuje się prawo składania prędkości, czyli przekształcenie Galileusza:

v = v’ + V.

Zasada względności Galileusza wymaga niezmienniczości praw przyrody względem tego przekształcenia.

Funkcja Lagrange’a dla cząstki swobodnej i układu cząstek

Biorąc pod uwagę jednorodność czasu i przestrzeni funkcja Lagrange’a dla cząstki swobodnej nie może zależeć w sposób jawny od wektora wodzącego ani do czasu. W związku z tym może być jedynie funkcją prędkości. Na skutek izotropowości przestrzeni nie może również zależeć od kierunku wektora prędkości, czyli może być jedynie funkcją jego wartości bezwzględnej czyli funkcją kwadratu prędkości. Funkcja Lagrange’a punktu swobodnego ma postać:

L = mv²/2

gdzie m jest masą punktu materialnego. Ponieważ mamy addytywność funkcji Lagrange’a to dla układu punktów nie oddziałujących ze sobą mamy:

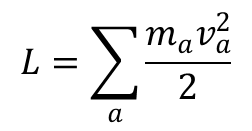Podana definicja masy ma sens jedynie przy uwzględnieniu addytywności funkcji. Masa nie może być ujemna, co wynika z zasady najmniejszego działania. Zgodnie z tą zasadą całka:

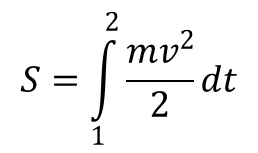opisująca działanie dla ruchu punktu materialnego, którego tor przechodzi przez punkty 1 i 2 ma minimum. Gdyby masa była ujemna, to dla torów w otoczeniu punktów 1 i 2 cząstka poruszałaby się bardzo prędko, a całka działania przyjmowałaby dowolnie duże, co do moduły, wartości. Innymi słowy nie miałaby minimum.

Rozpatrzmy teraz układ odosobniony, czyli taki w którym cząstki oddziałują ze sobą, ale nie podlegają wpływom żadnych ciał zewnętrznych. W takim wypadku można układ opisać funkcją Lagrange’a będącą suma funkcji dla układu cząstek nieoddziałujących oraz funkcji zależnej tylko od współrzędnych. Oznaczając te drugą funkcję literą U otrzymujemy:

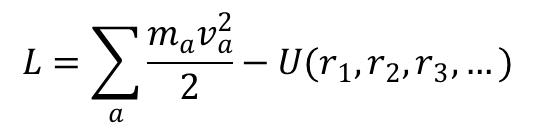gdzie r_a oznacza wektor wodzący. Pierwszy człon tego wyrażenia określa energię kinetyczną, a funkcja U energię potencjalną układu. Ponieważ energia potencjalna zależy tylko od położeń wszystkich cząstek tworzących układ, to zmiana położenia jednego z elementów natychmiast wpływa na energię potencjalną całego układu. Inaczej mówiąc oddziaływanie rozprzestrzenia się natychmiastowo. Taki charakter oddziaływań występujący w mechanice klasycznej jest związany z bezwzględnością czasu i zasadą względności Galileusza, co leży u podstaw mechaniki klasycznej. Gdyby oddziaływania rozchodziły się ze skończoną prędkością, to była by ona różna w różnych poruszających się względem siebie układach odniesienia, co wynika jednoznacznie z reguły dodawania prędkości. W takim wypadku prawa ruchu ciał oddziałujących byłyby różne w różnych inercjalnych układach odniesienia, co przeczy zasadzie względności.

Kolejnym istotnym elementem jest fakt, że czas jest nie tylko jednorodny ale również izotropowy, czyli własności mechaniczne nie zależą od zwrotu czasu. Zmiana t na –t nie zmienia funkcji Lagrange’a, a zatem nie wpływa na równania ruchu. Innymi słowy wszystkie ruchy w mechanice kalsycznej sa odwracalne. Znając funkcję Lagrange’a możemy podać równania ruchu:

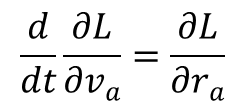czy też w postaci równań Newtona:

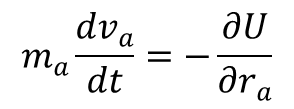Wektor znajdujący się po prawej stronie tego równania jest siłą oddziałującą na a-tą cząstkę. Siła zależy, podobnie jak energia potencjalna, tylko od współrzędnych wszystkich cząstek, a nie zależy od ich prędkości. Jednocześnie z powyższego wzoru wynika, że wektory przyspieszeń cząstek są funkcjami jedynie współrzędnych. Energia potencjalna jest określona z dokładnością do stałej addytywnej, której dodanie nie zmienia równań ruchu. Przyjmujemy, że energia potencjalna dąży do zera gdy odległość pomiędzy cząstkami się zwiększa.  Jeżeli przy opisie ruchu posługujemy się nie współrzędnymi kartezjańskimi, a współrzędnymi uogólnionymi funkcja Lagrange’a przyjmuje postać:

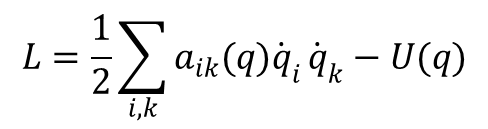gdzie a_ik są funkcjami tylko współrzędnych.

Weźmy teraz pod uwagę układ nieodosobniony A oddziałujący z układem B wykonującym dany ruch. Jest to przypadek, w którym układ A porusza się w polu zewnętrznym wytworzonym przez układ B. Równania ruchu znajduje się wychodząc z zasady najmniejszego działania wariując każdą ze współrzędnych niezależnie. Funkcję Lagrange’a układu A znajdujemy posługując się funkcją całego układu A + B, podstawiając w miejsce współrzędnych q_B dane funkcje czasu. Jeżeli układ A + B jest odosobniony mamy:

gdzie pierwsze dwa wyrazy są energiami kinetycznymi układów A i B, a trzeci określa wspólną energię potencjalną. Teraz zamiast współrzędnych uogólnionych q_B wstawimy dane funkcje czasu i pominiemy wyraz dotyczący znanej energii kinetycznej układu B otrzymujemy:

Jak widać ruch układu w zewnętrznym polu opisuje taka sama funkcja Lagrange’a z tą różnicą, że teraz energia potencjalna zależy w sposób jawny od czasu. W przypadku pojedynczej cząstki w zewnętrznym polu ogólna postać funkcji Lagrange’a ma postać:

a równania ruchu:

Pole, w którego wszystkich punktach działa na cząstkę ta sama siła nosi nazwę pola jednorodnego. W takim przypadku siła jest równa: U = – Fr.