Principles of Chemistry
Prawa zachowania
Podczas ruchu układu mechanicznego jego zachowanie jest określone przez 2s wielkości takich jak współrzędne uogólnione i ich pierwsze pochodne po czasie. Wielkości te ulegają zmianie w czasie. Jednak istnieją funkcje tych wielkości, które podczas ruchu zachowują stałą wartość zależną jedynie od warunków początkowych. Funkcje te noszą nazwę całek ruchu. Liczba niezależnych całek ruchu układu odosobnionego jest równa 2s – 1. Wśród całek ruchu istnieją takie, których stałość jest związana z jednorodnością i izotropowością czasu i przestrzeni. Odpowiadające tym całkom wielkości są addytywne, czyli ich wartość dla układu złożonego z nieoddziałujących ze sobą części jest równa sumie wartości dla każdej z części. Addytywność jest istotną cechą gdyż to dzięki niej można wyciągnąć szereg wniosków dotyczących stanu ciał, które wcześniej oddziaływały ze sobą na podstawie ich stanu przed wystąpieniem oddziaływania.
Rozpatrzmy zasadę zachowania wynikającą z jednorodności czasu. Dzięki tej jednorodności funkcja Lagrange’a układu odosobnionego nie zależy w sposób jawny od czasu. W związku z tym pochodna czasowa funkcji L ma postać:
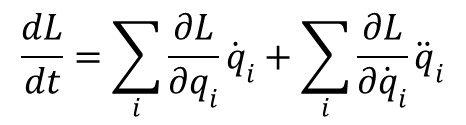Wstawmy do równania pochodną po czasie funkcji L:
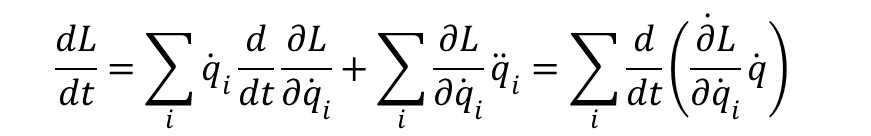co można przedstawić w formie:
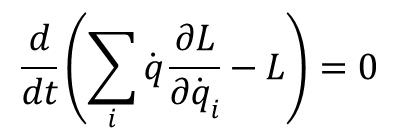Wyrażenie w nawiasie jest całką ruchu układu odosobnionego i nosi nazwę energii układu. Addytywność energii wynika bezpośrednio z addytywności funkcji Lagrange’a. Zasada zachowania energii jest spełniona nie tylko dla układów odosobnionych lecz również dla układów znajdujących się w stałym, czyli niezależnym od czasu, polu zewnętrznym. Wynika to z faktu, że w takim wypadku funkcja L nie zależy jawnie od czasu co jest jedynym warunkiem jaki został wykorzystany przy wyprowadzaniu zasady zachowania energii. Energię układu przedstawia suma dwóch różnych wyrazów; energii kinetycznej zależnej od prędkości i energii potencjalnej zależnej tylko od współrzędnych.
Pęd
Z jednorodności czasu wynika zasada zachowania energii układu. Natomiast z jednorodności przestrzeni wynika, że własności mechaniczne układu nie zmieniają się przy dowolnym równoległym przesunięciu całego układu. W takim razie rozpatrzmy nieskończenie małe przesunięcie układu o odcinek ;ε i zażądajmy aby funkcja Lagrange’a nie zmieniała się przy takim przesunięciu. Równoległe przesunięcie polega na przesunięciu wszystkich punktów układu o ten sam odcinek, czyli promienie wodzące zmieniają się ra ;→ ra + ε. Prędkości cząstek pod wpływem takiego przesunięcie nie ulegają zmianie, a funkcja Lagrange’a zmienia się o wielkość:
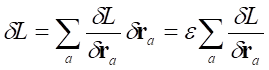Na podstawie równań Lagrange’a otrzymujemy:
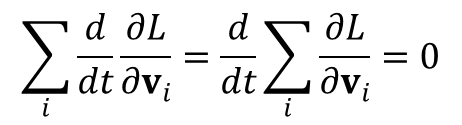czyli w odosobnionym układzie mechanicznym wielkość wektorowa:
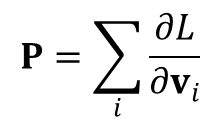nie zmienia się w trakcie ruchu. Wektor P nosi nazwę pędu układu. Różniczkując funkcję L widzimy, że pęd zależy od prędkości punktów materialnych w sposób:
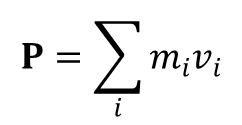Poza oczywistą addytywnością pędów istotnym jest, że pęd układu jest równy sumie pędów (w przypadku energii mamy dwie jej postacie), niezależnie od zachodzącymi pomiędzy nimi oddziaływania. Zasada zachowania pędu nie obejmuje jego wszystkich składowych przy wstępowaniu pola zewnętrznego. Jednak poszczególne składowe pędu mogą być zachowane również w polu zewnętrznym, pod warunkiem, że energia potencjalna nie zależy od którejś ze współrzędnych kartezjańskich. Przy przesunięciu wzdłuż tej osi współrzędnych kartezjańskich właściwości mechaniczne układu nie zmieniają się i tym samym rzut pędu na tę oś zostaje zachowany.
Biorąc pod uwagę dowolność wyboru osi równanie
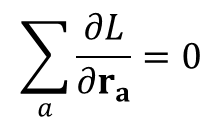ma proste wyjaśnienie fizyczne. Otóż pochodna jest równa sile działającej na a–tą cząstkę. Innymi słowy suma sił działających pomiędzy cząstkami tworzącymi układ odosobniony jest równa zero. To implikuje znane stwierdzenie, znane jako równość akcji i reakcji. Opis ruchu przy użyciu współrzędnych uogólnionych pokazuje, że pochodna pędu danej cząstki po czasie jest równa sile stowarzyszonej z daną cząstką.
Środek masy
Pęd odosobnionego układu ma różne wartości w różnych inercjalnych układach odniesienia. Jeżeli jeden układ porusza się względem drugiego z prędkością V, to prędkości cząstek v1 i v1’ względem tych układów spełniają związek v1= v1’ + V. Z tego powodu pędy w tych układach są związane zależnością:
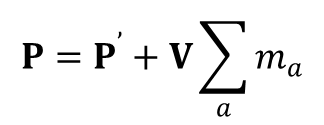Istnieje zawsze taki układ, w którym całkowity pęd jest równy zero. Prędkość takiego układu łatwo wyznaczyć z powyższego wzoru:
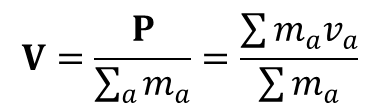Jeżeli całkowity pęd układu mechanicznego jest równy zeru, to układ punktów spoczywa względem odpowiedniego układu odniesienia. Podobnie prędkość dana powyższym wzorem określa prędkość ruchu całego układu o pędzie różnym od zera. Teraz zasadę zachowania pędu można sformułować w następujący sposób: środek masy układu odosobnionego porusza się ruchem jednostajnym prostoliniowym. Układ odniesienia, w którym środek masy spoczywa jest najdogodniejszy do opisu układów mechanicznych. Energia układu spoczywającego jako całości nosi nazwę energii wewnętrznej i jest sumą energii kinetycznej ruchu względnego cząstek układu oraz energii potencjalnej określającej ich wzajemne oddziaływanie. Jeżeli układ się porusza to jego energię określa suma energii wewnętrznej i energii kinetycznej.
Moment pędu
Z izotropowości przestrzeni wynika, że właściwości układu odosobnionego nie zmieniają się przy dowolnym obrocie. W związku z tym rozpatrzmy nieskończenie mały obrót przy którym nie ulega zmianie funkcja Lagrange’a. Nieskończenie mały obrót opisujemy wektorem δφ równoległym do osi obrotu, którego wartość jest równa kątowi obrotu δφ.
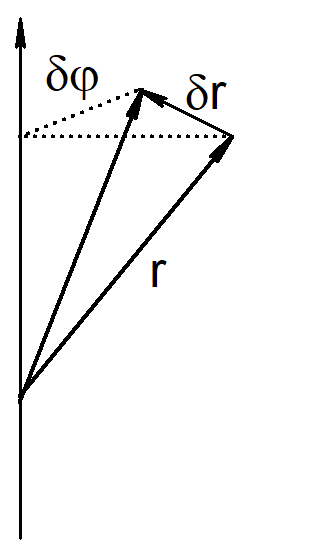Liniowa część przyrostu, w trakcie obrotu, wektora wodzącego wyrażona przez kat obrotu wynosi
|δr|= r sinθδφ
Wektor δr jest prostopadły do płaszczyzny przechodzącej przez r i δφ i dlatego
δr = [δφr]
Podczas obrotu układu zmieniają kierunek nie tylko wektory wodzące lecz również wektory prędkości wszystkich cząstek układu, przy czym przyrosty prędkości względem nieruchomego układu współrzędnych są równe:
δv = [δφv]
Warunek niezmienniczości funkcji Lagrange’a przy obrocie ma postać:
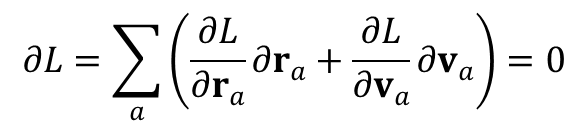Pochodna cząstkowa po prędkości to pęd, a po promieniu wodzącym to pierwsza pochodna pędu po czasie. Wstawiając do wzoru wyznaczone wcześniej wartości δr i δv otrzymujemy:
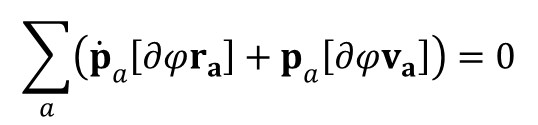lub też po zmianie kolejności czynników:
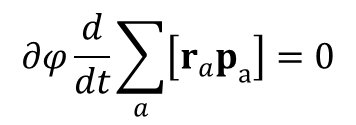Biorąc pod uwagę, że wielkość δφ jest dowolna, to w trakcie ruchu układu odosobnionego zachowana jest wielkość wektorowa:
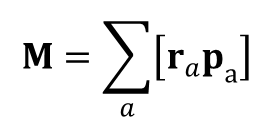która nosi nazwę momentu pędu. Wielkość ta jest oczywiście addytywna i nie zależy od oddziaływania pomiędzy cząsteczkami.
Podsumowując dotychczasowe rozważania można stwierdzić, że każdy układ odosobniony ma siedem całek ruchu: całkę energii, sześć całek pędu i moment pędu.
Ponieważ moment pędu jest określony za pomocą wektorów wodzących cząstek to jego wartość zależy od wyboru układu współrzędnych. Ponieważ wektory wodzące tego samego punktu materialnego wyprowadzone z początków różnych układów współrzędnych pomiędzy którymi odległość wynosi α spełniają zależność ra = ra’ + α, to
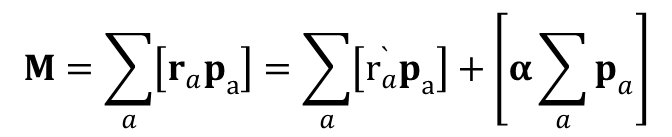lub
M = M’ + [aP]
Tak więc jedynie w przypadku układów spoczywających jako całość moment pędu nie zależy od wyboru początku układu współrzędnych.
W układach odosobnionych wszystkie składowe momentu pędu względem dowolnego punktu obranego jako początek układu współrzędnych są zachowane. Natomiast w polu zewnętrznym zawsze zachowany jest rzut momentu pędu na oś będącą osią symetrii danego pola, gdyż wtedy właściwości mechaniczne układu nie zmieniają się przy obrotach wokół tej osi. Szczególnym przypadkiem jest pole o centralnej symetrii czyli takie, w którym energia potencjalna zależy tylko od odległości od określonego punktu będącego centrum pola. Podczas ruchu w takim polu rzuty momentów pędu na dowolną oś przechodzącą przez centrum pola są zachowane. Inaczej mówiąc zachowany zostaje wektor momentu pędu określonego względem centrum pola. Natomiast nie zostaje zachowany wektor momentu pędu względem dowolnego punktu.