Pole krystaliczne

Orbitale atomowe (s, p, d, f itd.) są rozwiązaniami jednoelektronowego równania Schrödingera:

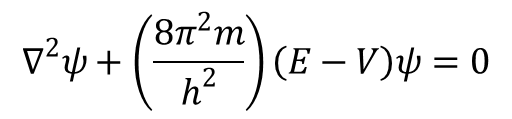
gdzie E oznacza energię całkowitą, V energię potencjalną, a ∇ jest operatorem Laplace’a (∂²/∂x + ∂²/∂y + ∂²/∂z). Równanie to można zapisać w formie:

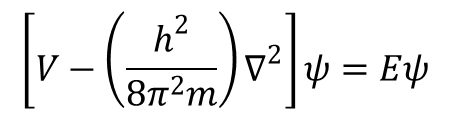
lub jako HΨ=Eψ, gdzie H jest operatorem Hamiltona. Dla atomu wodoru, pomijając sprzężenie spinowo-orbitalne, hamiltonian ma postać:

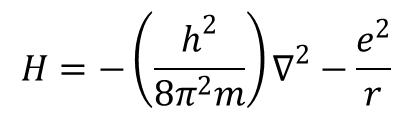
gdzie pierwszy czynnik wyraża energię kinetyczną, a drugi energię potencjalną elektronu. Dla atomów wieloelektronowych równanie falowe Hψ = Eψ jest spełnione, ale hamiltonian ma postać:

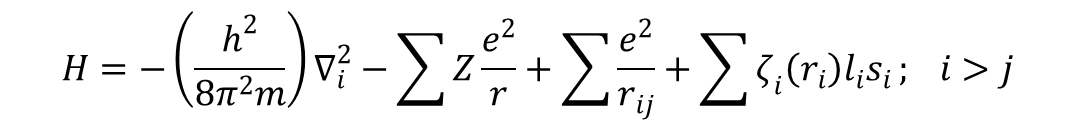
gdzie Z jest „efektywnym” ładunkiem jądrowym, r_i odległością i-tego elektronu od jądra, a r_ij. jest odległością między i-tym i j-tym elektronem. Pierwszy człon sumuje energię kinetyczną wszystkich elektronów, drugi sumuje przyciąganie wszystkich elektronów przez jądro, a trzeci sumuje wzajemne odpychanie między każdą parą elektronów. Czwarty człon opisuje sprzężenie między spinem a orbitalnym momentem magnetycznym (sprzężenie spinowo-orbitalne). Aby otrzymać całkowitą energię funkcji falowej należy przemnożyć obydwie strony  równania Schrödingera przez ψ otrzymując:

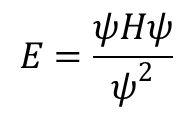
Ponieważ ψ jest funkcją współrzędnych przestrzennych, a E nie, zarówno licznik, jak i mianownik po prawej stronie równania można scałkować po całej przestrzeni, otrzymując:

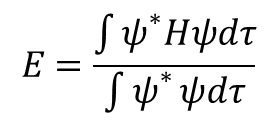
gdzie ψ^* jest funkcją sprzężoną do ψ. Mianownik jest równy jedności (∫ψ*ψdτ=1 ) jeżeli funkcja falowa jest unormowana, zatem:

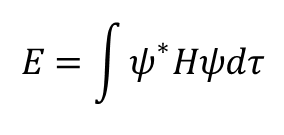
Równanie to ma fundamentalne znaczenie dla dyskusji o energiach funkcji falowych i stanów cząsteczek (złożonych z liniowych kombinacji funkcji falowych), ponieważ umożliwia określenie energii funkcji falowej, lub stanu, pod wpływem zaburzeń wywoływanych przez pewne pole zdefiniowane hamiltonianem H.

Wracając do równania na hamiltonian układu wieloelektronowego widzimy, że pierwsze dwa człony są wspólne dla wszystkich elektronów i niezależne od ich konfiguracji, a zatem nie wpływają na różnice energii stanów mierzone w widmie elektronowym. Trzeci człon, opisujący odpychanie między elektronami, opisuje stany spektroskopowe. Dla jonu d¹ jedynym możliwym stanem jest term ²D obejmujący dziesięć różnych stanów konfiguracji d¹ (m _l = 2, 1, 0, –1, –2, każdy z m _s = +½ lub –½). Ponieważ na powłoce walencyjnej znajduje się tylko jeden elektron, odpychanie z elektronami wewnętrznych powłok jest stałe i nie przyczyni się do obserwowanych różnic energii termów.

Gdy jon swobodny zostaje skompleksowany, energie układu określa zmodyfikowana postać  hamiltonianu:

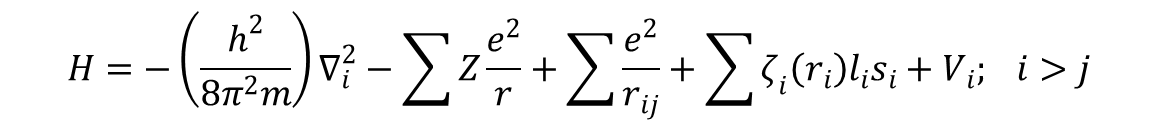
w którym pojawia się dodatkowy czynnik V_i, energia potencjalna w polu krystalicznym czyli energia oddziaływania elektronów z polem krystalicznym.

Teoria pola krystalicznego traktuje cząsteczkę tak, jakby składała się z dodatniego jonu metalu otoczonego ujemnie naładowanymi jonami (ligandami). Podejście to zostało zapoczątkowane przez Bethego i van Vlecka i było podstawą udanej analizy widm elektronowych oktaedrycznych jonów metali przejściowych. Teoria okazała się nieskuteczna w przewidywaniu bezwzględnej wielkości energii przejścia. To niepowodzenie nie jest zaskakujące, ponieważ kompleksy metali przejściowych niewątpliwie wykazują pewien stopień charakteru kowalencyjnego, a prosty model ładunku punktowego jest nieadekwatny do opisu tego typu układów. Niemniej jednak spektroskopia związków nieorganicznych (koordynacyjnych) rozwinęła się szybko po tym jak po raz pierwszy w roku 1951 (A. B. P. Lever) prawidłowo zidentyfikowano przejścia d–d na widmie absorpcyjnym. Rozwój ten wynikał w niemałej mierze z sukcesu, jaki odniosła teoria pola krystalicznego w przewidywaniu zarówno liczby przejść d–d, jak i ich względnych energii. Sukces ten wynikał z faktu, że teoria pola krystalicznego jest mocno oparta na geometrii, a raczej symetrii cząsteczki danego związku koordynacyjnego. Liczba stanów wzbudzonych, które generuje dana konfiguracja dⁿ, zależy wyłącznie od symetrii cząsteczki i jest całkowicie niezależna od jakiegokolwiek modelu używanego do opisu wiązań metal–ligand. Korzystając z symetrii, można obliczyć liczbę stanów wzbudzonych, a zatem ogólnie liczbę przejść elektronowych. Co więcej, korzystając z teorii pola krystalicznego można empirycznie określić ich względne energie. Chociaż ta prosta teoria nie daje możliwości określenia absolutnych wartości energii, dane eksperymentalne można wstawić do teorii w celu uzyskania półempirycznych parametrów radialnych, które odzwierciedlają oddziaływanie między metalem a ligandem. W układach wieloelektronowych, parametry odpychania elektronowego (parametry B i C Racah) pozwalają na dobre oszacowanie wyników eksperymentalnych.

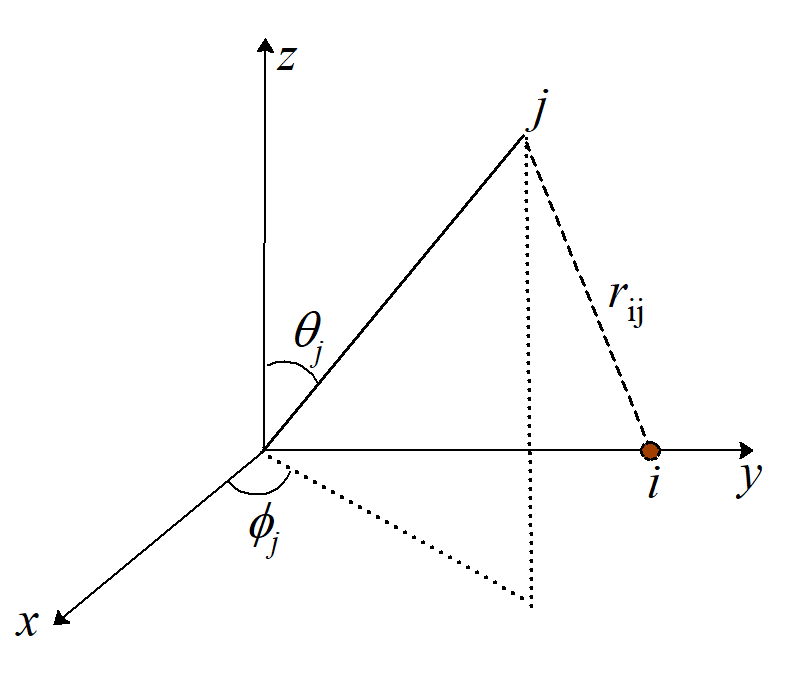Rysunek 1. Współrzędne elektronu j oraz liganda i w modelu ładunków punktowych

Energia związana z elektronem j w odległości r_ij od ujemnie naładowanego liganda i jest wyrażona jako:

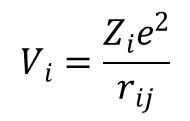
gdzie Z_i jest ładunkiem liganda. Zsumowanie potencjału wszystkich ligandów pozwala określić wypadkowy potencjał jaki działa na elektron w dowolnym polu cząsteczkowym. Teoria pola krystalicznego zakłada, że ligandy są ładunkami punktowymi lub dipolami punktowymi, a orbitale d są całkowicie niewiążące. Dla każdego elektronu d dodawana jest energia potencjalna wynikająca z pola krystalicznego i w ten sposób określane jest rozszczepienie tych orbitali. Jasnym jest, że rozszczepienie można przewidzieć jakościowo na podstawie teorii grup, ale znalezienie wartości energii rozszczepienia wymaga szczegółowego obliczenia potencjałów. Potencjał Ze/r_ij można zapisać w postaci harmonik sferycznych Y_kq(θ,ϕ). Ponieważ orbitale d można opisać w kategoriach harmonik sferycznych o źródle w jądrze metalu, wygodnie jest wyśrodkować harmoniki opisujące 1/r_ij w jądrze metalu. Wyrażenie na potencjał przyjmuje wówczas postać:

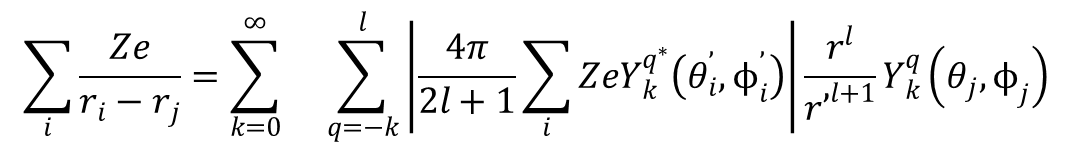
gdzie  odnosi się do ładunku liganda, a  do elektronu. Odległości radialne r’ i r są krótszym i dłuższym wektorem wodzącym łączącym źródło pola, w którym znajduje się elektron w atomie oraz odległość między elektronem a ładunkiem określającym ligand. Zwykle przyjmuje się, że elektron nie przemieszcza się zbyt daleko od jądra atomu metalu, tak że r odnosi się do odległości elektron-jądro. Pierwsza harmonika w powyższym równaniu opisuje współrzędne kątowe ładunku (liganda) i jest liczbą, którą można wyznaczyć określając odpowiednie wartości θ_i i ϕ_i na podstawie konkretnej budowy geometrycznej układu. Druga opisuje współrzędne kątowe elektronu, i z tego powodu jest związana z kątową częścią funkcji falowej danego elektronu. Harmoniki sferyczne można traktować jako funkcje opisujące fale stojące powstające na kuli zalanej wodą o jednakowej głębokości na całym obszarze. Harmoniczne i ich składowe mają zarówno wielkość, jak i kierunek, a dzięki odpowiedniej kombinacji dowolna geometria może być symulowana jako fala stojąca. Jednocześnie zestaw harmonik sferycznych może opisywać geometrię dowolnej cząsteczki.

Korzystając z powyższego równania można skonstruować operator Hamiltona, pozwalający na określenie energii danej konfiguracji elektronowej w dowolnym polu krystalicznym. Jako przykład wyprowadzimy hamiltonian dla pola o geometrii płaskiego kwadratu. Na początek zwróćmy uwagę, że w równaniu znajduje się suma od k = 0 do k = ∞. Ze względu na nieskończone sumowanie należy najpierw określić czy któreś ze składników sumy się zerują. 

Gdy znana jest postać hamiltonianu, energię dowolnej funkcji falowej można uzyskać poprzez obliczenie całki typu E=∫ψ*Hψdτ. Ogólnie rzecz biorąc, interesują nas różnice energii obserwowane w widmie elektronowym, a dla konfiguracji d¹ wystarczy wziąć pod uwagę udział V_i w H (pomijamy sprzężenie spinowo-orbitalne). Ponieważ funkcja falowa składa się zarówno z części radialnej, określającej odległość elektronu od jądra, jak i składowej kątowej, determinującej symetrię jego orbity, to postać całki określającej energię będzie zawierała składową radialną, która będzie skalarem i czynnik kątowy. Operator pola krystalicznego opisujący określoną geometrię jest liniową kombinacją harmonik sferycznych, które przekształcają się jako całkowicie symetryczna reprezentacja w danej grupie. Wynika to z faktu, że kształt cząsteczki jest niezależny od tego, czy jest odbijana w płaszczyźnie, czy też obracana wokół osi symetrii, a zatem wszystkie charaktery poszczególnych operacji symetrii danej grupy są jednostkowe, czyli mamy do czynienia z reprezentacją pełnosymetryczną. Jest to szczególnie istotna cecha operatora pola krystalicznego. Energia funkcji ψ zaburzonej przez operator pola krystalicznego jest określona przez całkę ∫ψ*Hψdτ. 

Wartość (wartość oczekiwana) całki jest liczbą, która również musi ulegać przekształceniom jako całkowicie symetryczna reprezentacja grupy. Liczba nie ulega zmianie przy obrotach lub odbiciu. Zatem iloczyn prosty reprezentacji ψ×H×ψ musi zawierać reprezentację pełnosymetryczną. To nakłada ścisłe warunki na charakter funkcji falowych, które mogą zostać sprzężone, oraz na postać samego hamiltonianu. Przykładowo, ponieważ orbitale d są symetryczne pod działaniem inwersji, tylko parzyste harmoniczne mogą mieć udział w hamiltonianie, czyli istotne są tylko harmoniki, których wartości k są parzyste. Harmoniczne z nieparzystą wartością k są typu ungerade; włączenie takich harmonicznych do hamiltonianu sprawi, że będzie on nieparzysty w odniesieniu do inwersji, a zatem nie będzie w stanie połączyć parzystych funkcji d, tym samym całka nie będzie już przekształcać się jako całkowicie symetryczna reprezentacja danej grupy. Ponadto funkcje o wartościach k większych niż 4 nie mogą łączyć dwóch orbitali d odpowiadających pobocznej liczbie kwantowej l=2. Dla funkcji orbitalnych f konieczne jest rozszerzenie hamiltonianu do k = 6.

W ten sposób suma w hamiltonianie zostaje zredukowana, dla orbitali d, do k = 0, 2 i 4. Wartość q reprezentuje rzut wektora k na oś z, tak jak magnetyczna liczba kwantowa m_l jest składowa z kątowej liczby kwantowej l. Należy teraz zastanowić się która z wartości q będzie wchodzić do hamiltonianu. W zasadzie mogą to być wszystkie wartości q. Jednak tam, gdzie główna oś symetrii jest parzysta w grupie punktowej symetrii cząsteczki, nieparzyste wartości składowej q nie wpływają na całkowicie symetryczną reprezentację. Składowe takie mają swój udział tylko w hamiltonianach obejmujących grupy, których oś główna jest nieparzysta, szczególnie w przypadku grup z główną osią trójkrotną. Powyższe stwierdzenie jest prawdziwe tylko wtedy, gdy główna oś symetrii jest zdefiniowana wzdłuż osi z, czyli osi wzdłuż której funkcje są kwantowane. Utworzenie hamiltonianu dla związku o kwadratowej (płaskiej) geometrii (D_4h) odbywa się poprzez obliczenie wyrażenia 

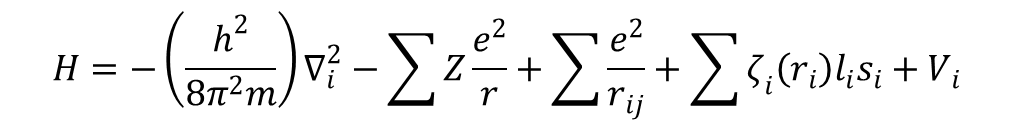
dla harmonik k = 2 (q = –2, 0, 2) i k = 4 (q = –4, –2, 0, 2, 4). Harmonika z k = 0 nie musi być brana pod uwagę, ponieważ jej działanie powoduje jedynie przesunięcie wszystkich poziomów d o tę samą wielkość, a tym samym nie przyczynia się do dyskusji na temat przejść elektronowych w obrębie orbitali d.

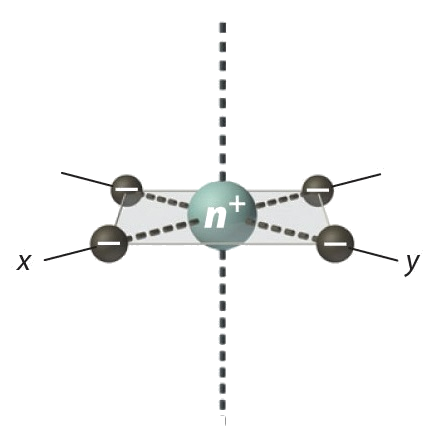Używając reprezentacji współrzędnych biegunowych, cztery ligandy leżą w płaszczyźnie xy pod kątem 90° do osi z (θ = 90 °). Wartości ϕ (kąt względem osi x, gdy ligand jest rzutowany na płaszczyznę xy) dla czterech ligandów będą wynosić odpowiednio 0°, 90°, 180° i 270°. Hamiltonian (potencjał) przyjmuje postać:

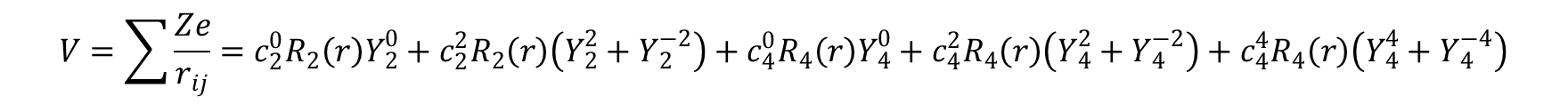
gdzie: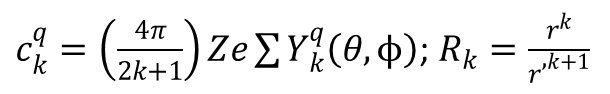 

a wkłady od składowych –2, +2 oraz –4, +4 jako równoważne zgrupowano ze sobą. Wartości c_k^q szacuje się sumując wkłady poszczególnych ligandów w sposób następujący:

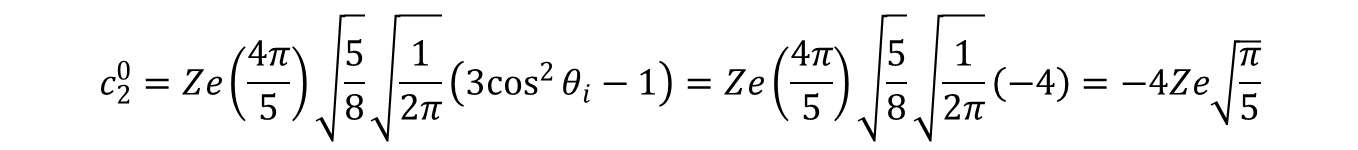
gdzie (–4) wynika z sumowaniu wkładów czterech ligandów dla których cos90 = 0;

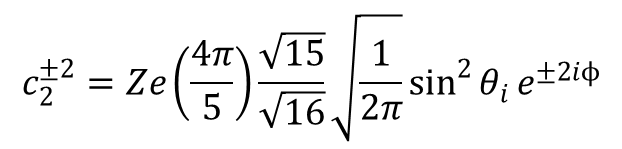
sumowanie po czterech ligandach prowadzi do:

ligand	θi	ϕi	c2±2	c4±2	c2±4
			sin2Θe±2iΦ	>sin2Θe±4iΦ	sin4Θe±2iΦ
1	90	0	1	1	1
2	90	90	–1	–1	1
3	90	180	1	1	1
4	90	270	–1	–1	1
		Razem:	0	0	4

 Sumy dla c₂±2 i c₂±4 są zerowe, nie wpływają na hamiltonian układu.

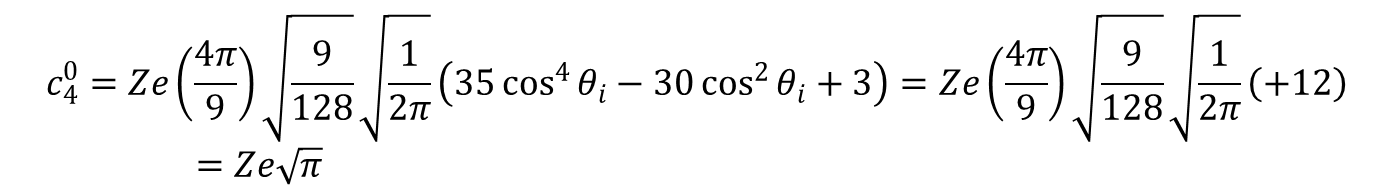
W tym przypadku, tak jak poprzednio, wyrazy zawierające cosθ wnoszą zerowe udziały.

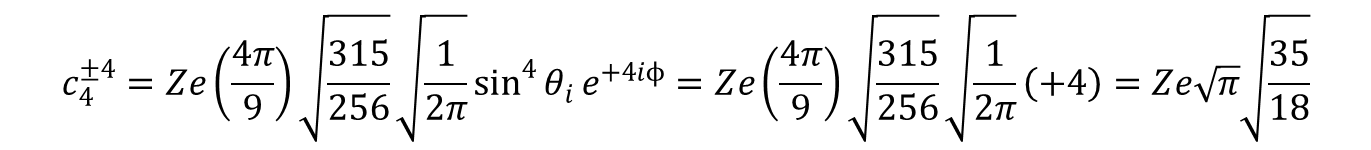
Łącząc poszczególne wyrażenia otrzymujemy hamiltonian dla geometrii płaskiego kwadratu (D_4h) w postaci:

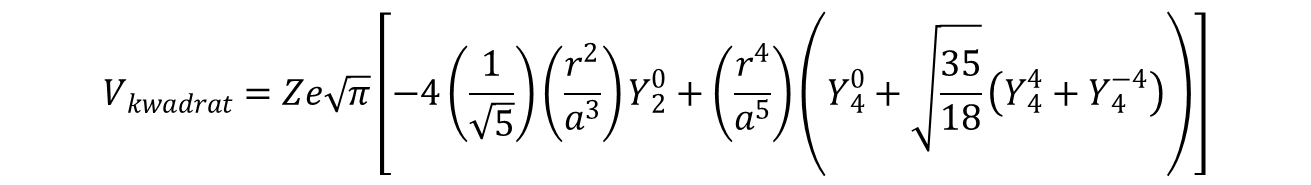
zawierającej wyrażenia radialne, a odległość między metalem a ligandem w płaszczyźnie jest oznaczona jako a.

Hamiltoniany dla innych geometrii związków koordynacyjnych są tworzone dokładnie w ten sam sposób, poprzez wstawienie współrzędnych kątowych ligandów i zsumowanie wyników. Hamiltonian dla kompleksu o geometrii oktaedrycznej (O_h) można otrzymać przez dodanie dwóch równoważnych ligandów, wzdłuż osi z czyli o współrzędnych (θ,ϕ) równych (0,0) i (180,0). Włączenie tych dwóch dodatkowych ligandów osiowych powoduje zerowanie sumowania c₂⁰, pozostawiając wyrażenia rzędu 4, a mianowicie:

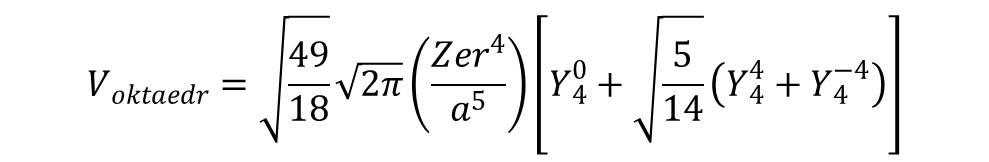
Jeśli dwa ligandy wprowadzone w pozycjach aksjalnych nie są takie same jak te w płaszczyźnie ekwatorialnej i/lub leżą w różnych odległościach, to związek nadal należy do grupy D_4h (zakładając zachowanie kątów 90° i równoważność ligandów osiowych) będąc przedstawicielem powszechnie występującej klasy tetragonalnych związków typu trans-ML₄Z₂. Długość wiązania metal–ligand dla ligandów na osi z, o współrzędnych (0,0) i (180,0) oznaczymy jako b, co prowadzi do hamiltonianu postaci:

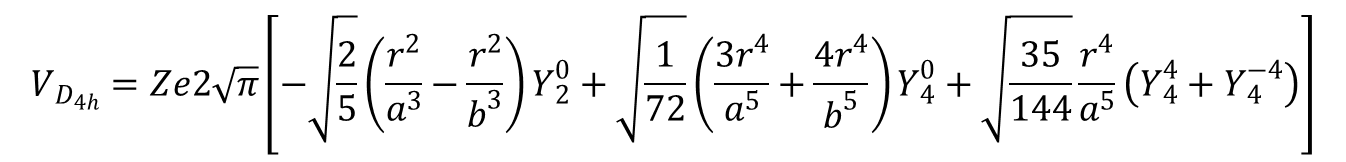
Ten hamiltonian przekształca się do równania opisującego płaski kwadrat przez pominięcie wyrażeń z b, oraz do wyrażenia na V_oktaedr gdy a = b. Często wygodnie jest traktować cząsteczkę trans-ML₄Z₂ jako oktaedr zaburzony tetragonalnie. W takim wypadku równanie powyższe można przekształcić wydzielając hamiltonian dla oktaedru w następujący sposób:

V_D4h = V_Oh + V_tetragonal

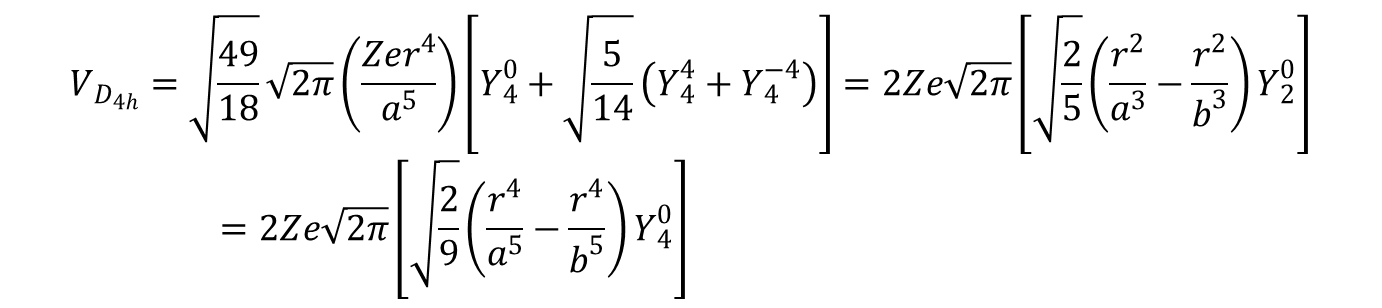 Przed zastosowaniem powyższych hamiltonianów warto wykorzystać korzyści jakie daje rozpatrzenie symetrii. Użyte harmoniki należą do grupy sferycznej R₃ i obejmują w niej termy S, P, D, F itd., zgodnie z ich wartościami k (lub, jak zazwyczaj zapisujemy L, czyli całkowity orbitalny moment pędu). W rzeczywistych cząsteczkach harmoniczne będą obejmować reprezentacje w ramach odpowiedniej grupy punktowej. Do hamiltonianu mogą zatem wejść tylko te harmoniki, które obejmują całkowicie symetryczną reprezentację w danej grupie punktowej. W związku z tym dla oktaedru termy w grupie O_h korelują z wymienionymi termami w grupie R₃ (symboli parzystości „g”, „u” nie zapisujemy, ponieważ zależą od tego, czy zaangażowane są orbitale d lub p):

S	L=0	A1
P	L=1	T1
D	L=2	T2 + E
F	L=3	A2 + T1 + T2
G	L=4	A1 + E + T1 + T2

co pokazuje, że jedynie harmoniki L = 0 i L = 4 wchodzą do hamiltonianu pola o symetrii oktaedrycznej.

Obliczanie elementów macierzowych – układy sześcienne

Istnieją bardzo wydajne i stosunkowo proste metody oceny całek pola krystalicznego. Zanim przejdziemy do omówienia tematu warto przedstawić zagadnienia dotyczące pojęcia elementu macierzowego w kontekście rozważanego problemu. Rozważmy funkcję falową ψ, która może być składnikiem bazy ψ_i (i = 1, 2, 3, …, n) służącej do opisu funkcji w jakimś ogólnym układzie. Funkcją może być orbital atomowy opisany przez jego liczbę kwantową l i magnetyczną liczbę kwantową m_l; przykładowo funkcja w notacji |l,m_l>, postaci |2,2> opisuje orbital d. Funkcją taką może być składowa termu opisana liczbami kwantowymi |LSM_LM_S>, np. term ³F zapisany w formie |3,1,1,1>, może to być orbital |xz> lub liniowa kombinacją kilku z tych możliwości. Wygodny jest zapis całek w postaci wprowadzonej przez Diraca, zgodnie z którym

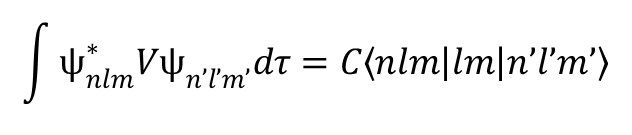
gdzie składowe radialne i kątowe całki po lewej stronie zostały rozdzielone na skalar (liczbę) C, która zawiera informacje radialne, oraz symbol, który zawiera wszystkie informacje kątowe. Zwróćmy uwagę, że nawias bra, <nlm|, określa sprzężenie funkcji falowej o liczbach kwantowych n, l i m, podczas gdy ket |n'l'm’> zawiera funkcję falową z liczbami kwantowymi n', 1' i m' (odpowiednio główną, orbitalną i magnetyczną). Ponadto, ponieważ operator pola krystalicznego jest wyrażony w postaci harmonik sferycznych, można je również zdefiniować za pomocą odpowiadającym im wartości l i m. Zauważmy, że zapis Schrödingera po lewej stronie równania jest wyrażony w przestrzeni położeń, podczas gdy symbol Diraca po stronie prawej jest zdefiniowany w przestrzeni pędów. Wartość liczbową symbolu Diraca można obliczyć łącząc momenty kątowe wyrażone przez kwantowe liczby kątowe funkcji falowych i operatora. Całka po lewej stronie jest zdefiniowana w jednostkach  energii (hamiltonian), podczas gdy w zapisie Diraca po stronie prawej energia jest zawarta w C, a funkcja w nawiasach jest pozbawionym jednostki współczynnikiem kątowym, czyli bezwymiarowym skalarem. Wartości oczekiwane całek pola krystalicznego potraktujemy jako elementy formalizmu macierzowego Diraca i przedstawimy w postaci parametrów radialnych. Ponadto, dla uproszczenia, wielkości tych elementów przedstawimy w postaci takiej jak <2|V|2> = Dq, co nie jest ściśle poprawne, ponieważ wielkość <2|H|2> jest po prostu liczbą. Natomiast stosujemy skróconą notację poprawnego zapisu postaci C<2|V|2> = Dq×1. Należy również zwrócić uwagę na symetrię funkcji. Orbital |x² – y²> ze względu na symetrię stanowi odrębny element w grupie D_4h (przekształca się jako b₁), ponieważ brak jest w tej grupie operacji, które przekształcają ten orbital w inny. Podobnie para orbitali d opisanych funkcjami falowymi |xz,yz> (przekształcająca się jak e_g) pod względem symetrii stanowi element grupy D_4h, ponieważ żaden operator tej grupy nie może przekształcić ich w inne orbitale. Jednak funkcja orbitalna |xz> nie stanowi elementu nieprzywiedlnego grupy D_4h, ponieważ operator C₄. przekształca ją w |yz>. Jeśli dana funkcja ma symetrię zgodną z nieprzywiedlnym elementem grupy, przykładowo x² – y², to danej reprezentacji odpowiada tylko jedna taka funkcja, a jej energia w polu krystalicznym, V, jest bezpośrednio określana przez wartość tej funkcji. Można to napisać w postaci:

Załóżmy, że mamy do czynienia z grupą C_2v. W tabeli charakterów grupy znajdujemy, że x² – y² (a₁) przekształca się w taki sam sposób jak z² (a₁). Zatem funkcja <x² – y²| V |z²> również przekształca się jako a₁ (pamiętajmy, że V również musi mieć symetrię a₁) i dlatego jej wartość nie musi być zerowa i generalnie nie będzie równe zero. W tym przypadku pole krystaliczne łączy dwa orbitale tworząc poziom dwukrotnie zdegenerowany. Aby ocenić stopień degeneracji i energie powstałych orbitali konieczne jest skonstruowanie wyznacznika sekularnego postaci:

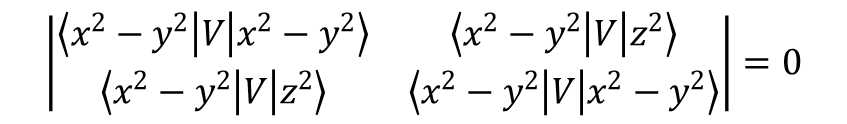
Pierwiastki tego wyznacznika to dwie wartości E odpowiadające w tym przypadku energiom dwóch par orbitali będących kombinacją x² – y² z pewnym udziałem z² oraz z² z pewnym udziałem x² – y². Określenie stopnia zmieszania orbitali jest możliwe po wprowadzeniu energii do pary równań wyrażonych w wyznaczniku. Generalnie dążymy do tego aby wyrazy na przekątnej macierzy były niezerowe przy jednoczesnym zerowaniu wyrazów niediagonalnych. Diagonalizacja macierzy daje nam bezpośredni dostęp do pierwiastków wyznacznika. Na przykład, aby określić, jak pięć orbitali d opisanych wyrażeniem |2,m_l> gdzie m_l = 2, 1, 0, –1, –2 zachowuje się w oktaedrycznym polu krystalicznym, konieczne jest obliczenie zbioru elementów macierzy <m_l|V|m_l’> ponieważ te pięć funkcji w różny sposób reaguje na symetrię pola oktaedrycznego, i operator pola krystalicznego powoduje ich rozdzielenie. W notacji Diraca macierz przyjmuje postać:

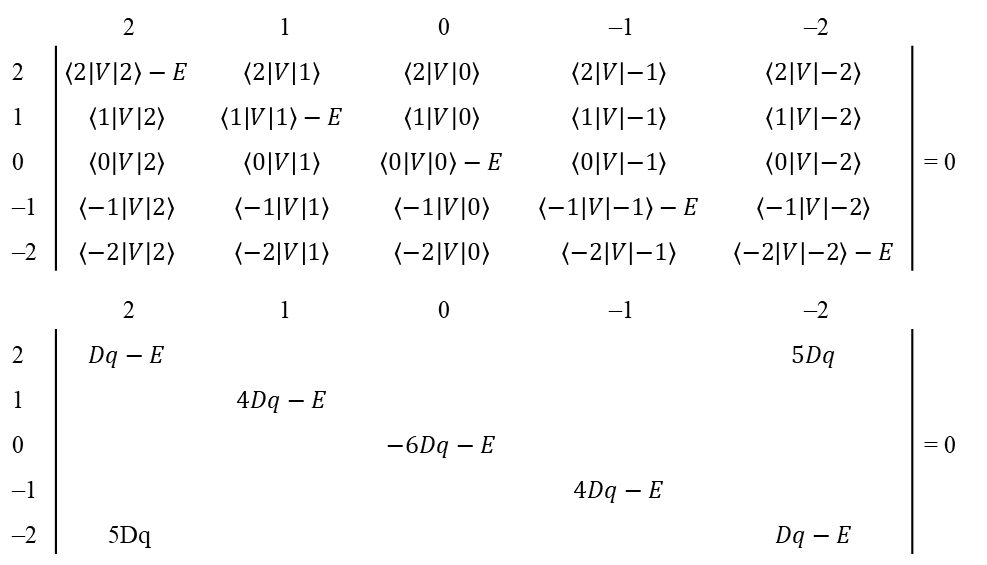
z czego można wywnioskować, że funkcje d | 2,1>, | 2,–1> i | 2,0> są pod względem symetrii zgodne z symetrią oktaedrycznego pola krystalicznego i mają energie <1| V|1> = <–1|V|–1> = –4Dq i <0|V|0> = 6Dq. Nie występują niezerowe elementy typu <1|V|–1> lub <1|V|0>, które mieszałyby te funkcje. Z drugiej strony istnienie niezerowej wartości dla <2|V|–2> wymaga zmieszania orbitali d |2,2> i | 2,–2> z energiami odpowiadającymi pozostałym dwóm pierwiastkom wyznacznika, odpowiednio 6Dq i –4Dq. Ten wynik uzyskuje się diagonalizując podwyznacznik:

 

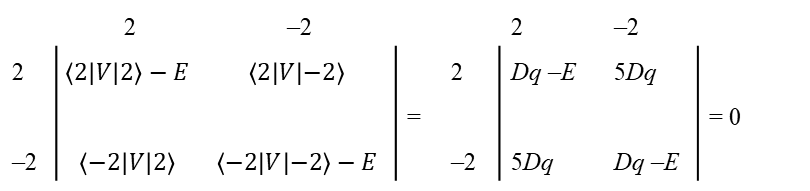
czyli wyznacznik 2 x 2 postaci:

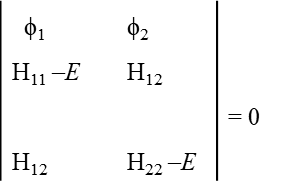
w przypadku którego wartości energii są równe E = H₁₁ – H₁₂ cotθ i E = H₂₂ – H₁₂, a funkcje falowe (wektory własne) postaci: ψ₁ =sinθψ₁ – cosθψ₂ i ψ₂ = cosθψ₁ + sinθψ₂

Ogólnie każdy problem wymaga skonstruowania i diagonalizacji jednego lub więcej wyznaczników sekularnych zawierających zbiór elementów macierzowych obejmujących odpowiedni operator i zbiór funkcji bazowych. W celu opracowywanie metod oceny wielkości elementów macierzy, konieczne jest bliższe przyjrzenie się postaci analitycznej funkcji bazowych i operatora. Chcemy wyprowadzić działanie hamiltonianu pola oktaedru na orbitale d, czyli oszacować wielkości elementów macierzowych <m|V|m'>. Szczegółowe oszacowanie elementu macierzowego można rozpatrywać na dwa sposoby. Można je traktować jako całkę Schrödingera będącą całką iloczynu trzech funkcji, z których każda może być zapisana jako kombinacja harmonik sferycznych. Alternatywnie można rozpatrywać to zagadnienie w przestrzeni pędów w notacji Diraca, jako sprzężenie dwóch pędów kątowych w celu uzyskania wypadkowej. Pierwsze, klasyczne, podejście można przedstawić następująco. Hamiltonian H zawiera, przedstawione powyżej, hamiltoniany pola krystalicznego i przyjmuje, że pole elektryczne doświadczane przez elektrony jest zdefiniowane przez H = ev. Orbitale d przestawiają formy analityczne:

 

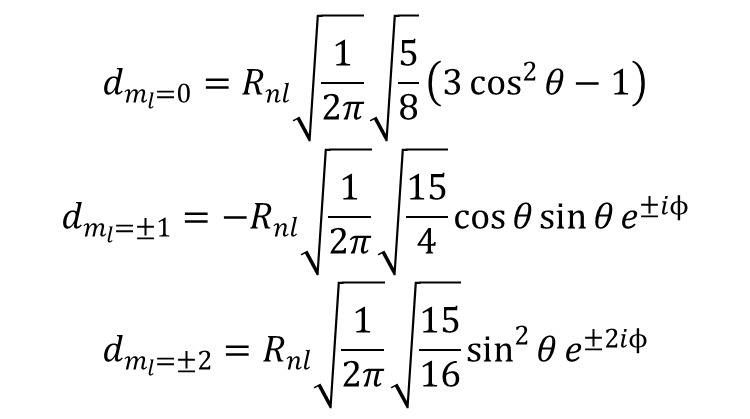
Rozważmy energię orbitalu d o m₁ = 0, co odpowiada d_z² w polu oktaedrycznym. Jeśli hamiltonian pola oktaedrycznego rozbijemy na składowe Y₄⁰ i Y₄⁴ , to składnik Y₄⁰ można zapisać jako:

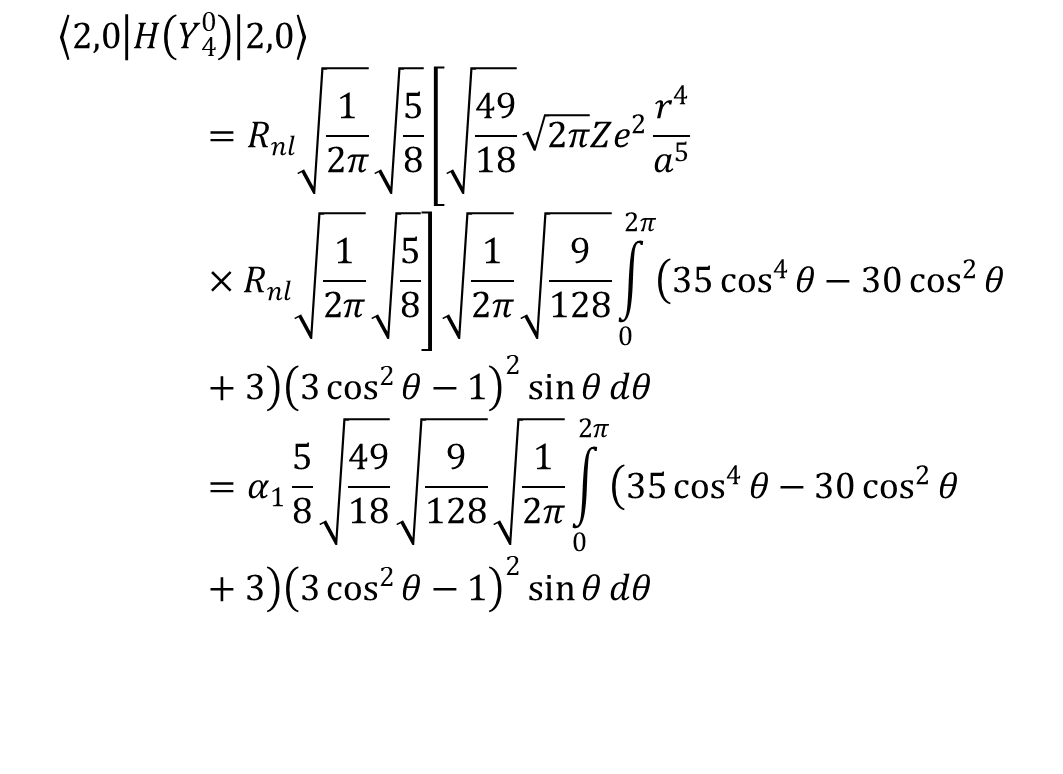
gdzie dla elektronów 3d mamy

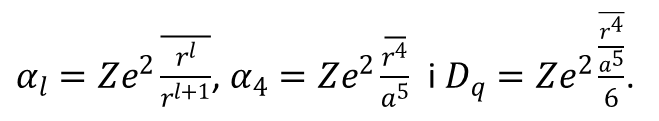
Obliczenia dla wszystkich typowych geometrii związków koordynacyjnych zostały oczywiście opublikowane. Energie funkcji falowych zaburzone polem krystalicznym są generalnie zapisywane w postaci parametrów radialnych pola, których wyrazy czwartego rzędu (a₄) są zawarte w powyższym równaniu. Parametr r⁴/a⁵ wyraża promień funkcji radialnej elektronu metalu, a mianownik i licznik są nierozłączne. Zdefiniowano kilka parametrów pola krystalicznego, z których najbardziej znanym jest Dq.

W przypadku d¹ konieczne jest jedynie odczytanie z widma eksperymentalnego energii dla rozszczepionych orbitali d, a tym samym uzyskanie wartości parametrów radialnych, które można wykorzystać jako parametry empiryczne, które jednak przekazują stosunkowo niewiele informacji chemicznych. Energie układów wieloelektronowych można również sparametryzować w kategoriach układów jednoelektronowych, a zatem w kategoriach różnych całek radialnych. Wartości oczekiwane elementów macierzy dla pozostałych orbitali d są wyrażone przez:

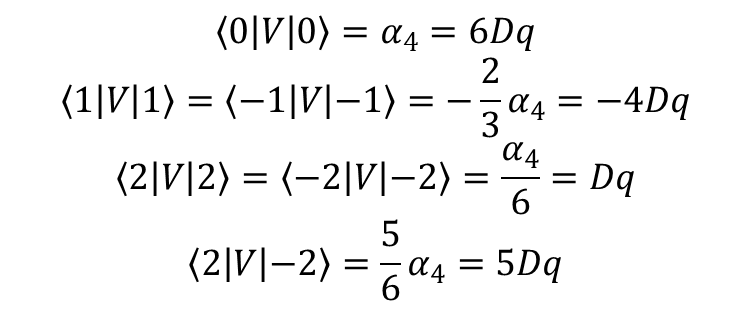
Należy zauważyć, że skoro składowe oktaedrycznego hamiltonianu (q) wynoszą 0, 4 i –4, to hamiltonian może łączyć tylko funkcje falowe, których wartości m różnią się o 0, 4 lub –4. To wyjaśnia fakt, że elementy macierzy, takie jak <1|V|0> i <l|V|–1> itd., z konieczności są równe zero, gdy V jest operatorem hamiltonianu pola oktaedrycznego. Zastosowanie powyższych rozważań do konkretnych orbitali d:

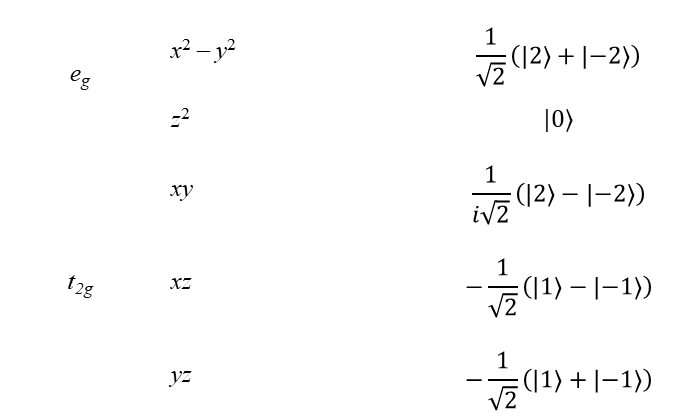
pokazuje znane rozszczepienie pięciu orbitali d w polu krystalicznym o symetrii oktaedrycznej czyli poziom t_2g o energii –4Dq i poziom e_g o energii 6Dq.

Elementy macierzowe układu tetragonalnego

Rozpatrując hamiltonian dla pola o symetrii D_4h, całki radialne należy zdefiniować z uwzględnieniem wyrazów drugiego rzędu, oraz dla dwóch różnych odległości metal-ligand, aksjalnych (Ax) (b) i ekwatorialnych (Eq) (a), zatem:

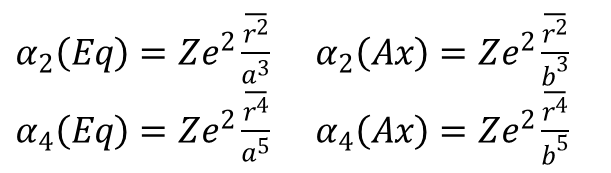
W widmie elektronowym na ogół nie ma wystarczających informacji, aby zidentyfikować wszystkie te parametry, więc zazwyczaj są one grupowane razem poprzez określenie nowej całki radialnej drugiego rzędu Ds i nowej całki rzędu czwartego Dt, zdefiniowanych jako:

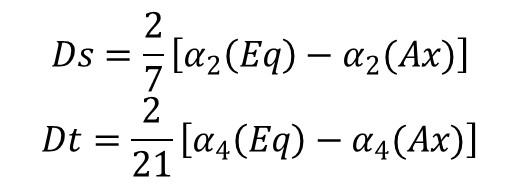
Współczynniki 2/7 i 2/21 występują często w obliczeniach, a ich uwzględnienie w definicjach upraszcza wzory opisujące energię. W ten sposób elementy macierzy orbitali d w polu o symetrii D_4h są określone jako:

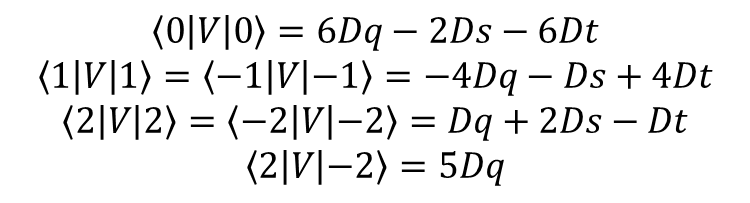
i dla konkretnych orbitali d mamy:

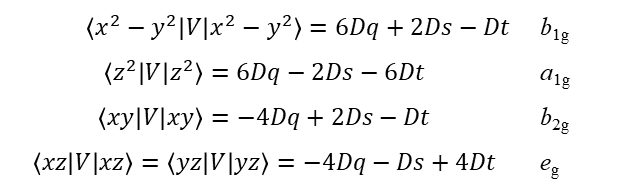
Ponieważ Dq zależy tylko od (a), która jest odległością wiązania metal-ligand w płaszczyźnie ekwatorialnej, wartość Dq w kompleksie o symetrii D_4h odnosi się tylko do ligandów w pozycjach ekwatorialnych. Zauważmy, że Dq ma dokładnie taką samą definicję jak w kompleksach o symetrii oktaedrycznej. Często okazuje się, że przechodząc od oktaedrycznego ML₆ do tetragonalnego trans-ML₄Z₂, wartość Dq (L) pozostaje w przybliżeniu stała. Dt jest różnicą dwóch parametrów czwartego rzędu i przez porównanie z definicją dla Dq jest oczywiste, że w polu o symetrii D_4h Dt można wyrazić poprzez ekwatorialne i aksjalne czynniki Dq, a mianowicie:

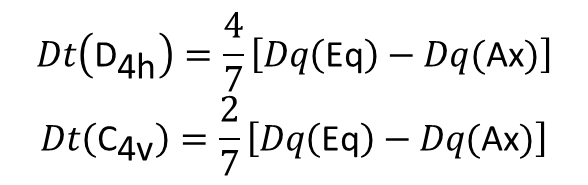
gdzie druga zależność opisuje kompleksy z jednym ligandem aksjalnym ML₅ (C_4v).

Układ trygonalny

Wiele związków koordynacyjnych, poczynając od związków z ligandami dwukleszczowymi typu [M(en)₃]²⁺ do związków o geometrii bipiramidy trygonalnej typu ML₅ posiada trójkrotną oś symetrii. Sposobem opisu kompleksów oktaedrycznych zaburzonych trygonalnie jest użycie trójkrotnej osi symetrii w oktaedrze jako osi kwantyzacji. W takim przypadku następuje zmieszanie orbitali d i powstają następujące hybrydy:

Przekształcające się jako t_2g:

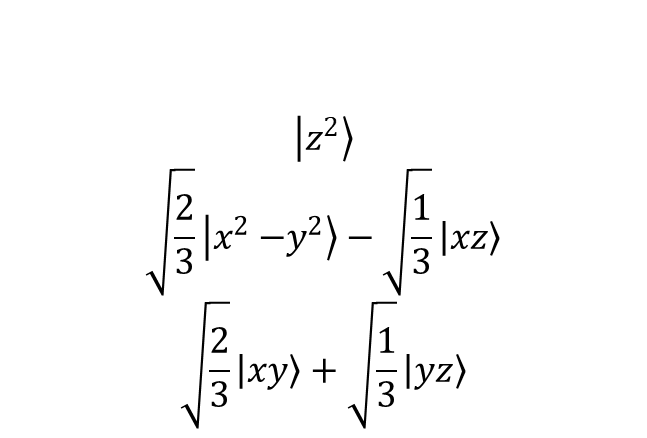
Przekształcające się jako e_g:

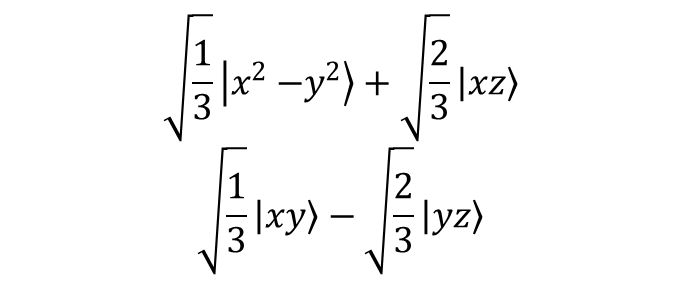
Zniekształcenie wzdłuż osi trójkrotnej znosi degenerację poziomu t_2g tworząc e + a₁; jednak poziom e_g pozostaje dwukrotnie zdegenerowany. W związku z tym w tego typu związkach pojawiają się trzy poziomy związane z orbitalami d, czyli a₁ + 2e. Definiuje się dwa dodatkowe parametry rozszczepienia związane ze zniekształceniem trygonalnym Ds i Dt, co prowadzi do rzeczywistych i urojonych elementów macierzy orbitali d dla składowej zniekształcenia trygonalnego pola:

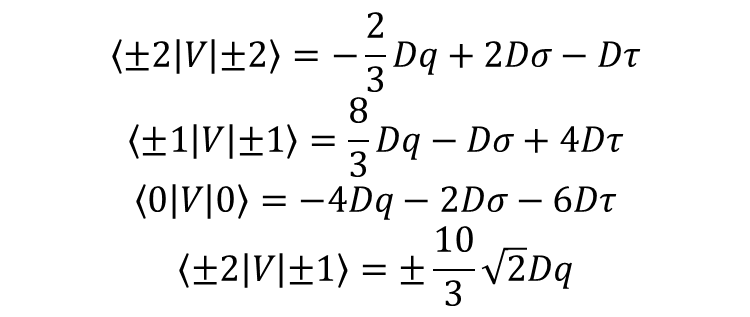
czyli:

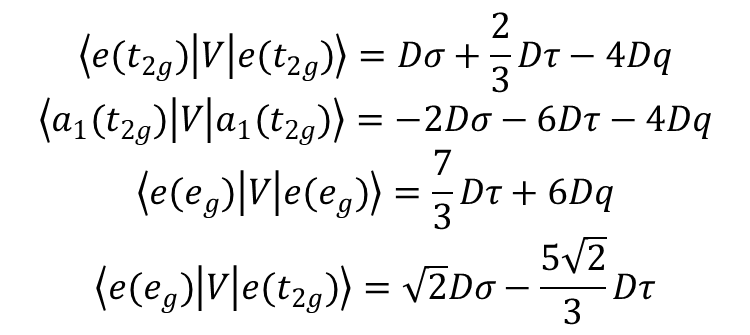
W przypadku bipiramidy trygonalnej (D_3h) energie orbitali d dane są wyrażeniami:

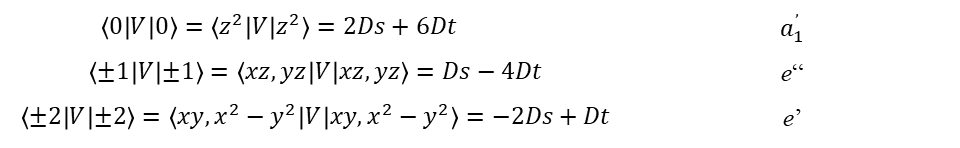
Grupy sześcienne (kubiczna O_h, oktaedryczna O_h i tetraedryczna T_d) generują zasadniczo ten sam rodzaj rozszczepiania, trójkrotnie zdegenerowany układ t₂ i dwukrotnie zdegenerowany poziom e, z wyjątkiem tego, że tetraedryczne i sześcienne rozdzielenie energii poziomów wynosi –4/9 i –8/9 wielkości odpowiadającej symetrii oktaedrycznej. Znak minus wskazuje, że mamy do czynienia z inwersją poziomów. Ponieważ rozszczepienie w tetraedrycznym kompleksie jest zwykle określane jako 10Dq_(tet), oczywistym jest oczekiwanie, że dla tetraedrycznego kompleksu ML₄ wartość Dq będzie wynosić około 4/9 wielkości odpowiadającej oktaedrycznemu kompleksowi ML₆. Pomimo prostoty podejścia jest to generalnie prawda.

Diagramy rozszczepienia w polu krystalicznym

Zastosowanie przedstawionej teorii do różnych stereochemii związków kompleksowych prowadzi do diagramów rozszczepienia orbitali d, które można wykorzystać do przewidywania absorpcyjnego widma elektronowego jonu metalu przejściowego w danym otoczeniu. Diagramy tego rodzaju można zwykle uzyskać odwołując się do prostych zależności wynikających z teorii grup jeżeli nie potrzebujemy wartości liczbowych parametrów energii i rozszczepienia. W związku z tym w niezaburzonym kompleksie oktaedrycznym (grupa punktowa O_h), w którym nie ma zróżnicowania między współrzędnymi x, y i z, orbitale xz, yz i xy leżące między tymi współrzędnymi muszą być nierozróżnialne, a zatem zdegenerowane (o równej energii). Dlatego też stanowią bazę trójwymiarowej reprezentacji w grupie punktowej O_h, czyli t_2g. W dalszej dyskusji zakładana jest ogólna znajomość teorii grup. Tabele charakterów grup podane zostały w Uzupełnieniu U.4. Kolejne dwa orbitale d, czyli z² i x²–y², leżą wzdłuż osi x, y i z. Ponieważ te osie są nierozróżnialne, wynika z tego, że te dwa orbitale są również nierozróżnialne i dlatego stanowią podstawę dla dwuwymiarowej reprezentacji, mianowicie e_g. Dwa zestawy orbitali można rozróżnić ponieważ pierwszy leży między osiami, a drugi wzdłuż nich. Elektron na poziomie e_g jest skierowany bezpośrednio na ligand reprezentowany w teorii pola krystalicznego przez ładunek punktowy, dlatego ulegałby większej destabilizacji niż elektron na poziomie t_2g, który znajduje się pomiędzy ligandami; dlatego poziom e_g ma wyższą energię niż t_2g. Taki sam jakościowy wynik uzyskuje się w wyniku analitycznego rozwiązania równań pola krystalicznego, ale rozważenie symetrii pozwala uzyskać rezultat szybciej i mniejszym nakładem pracy.

Rozszczepienie w polu krystalicznym o symetrii D3h (bipiramida trygonalna)

 

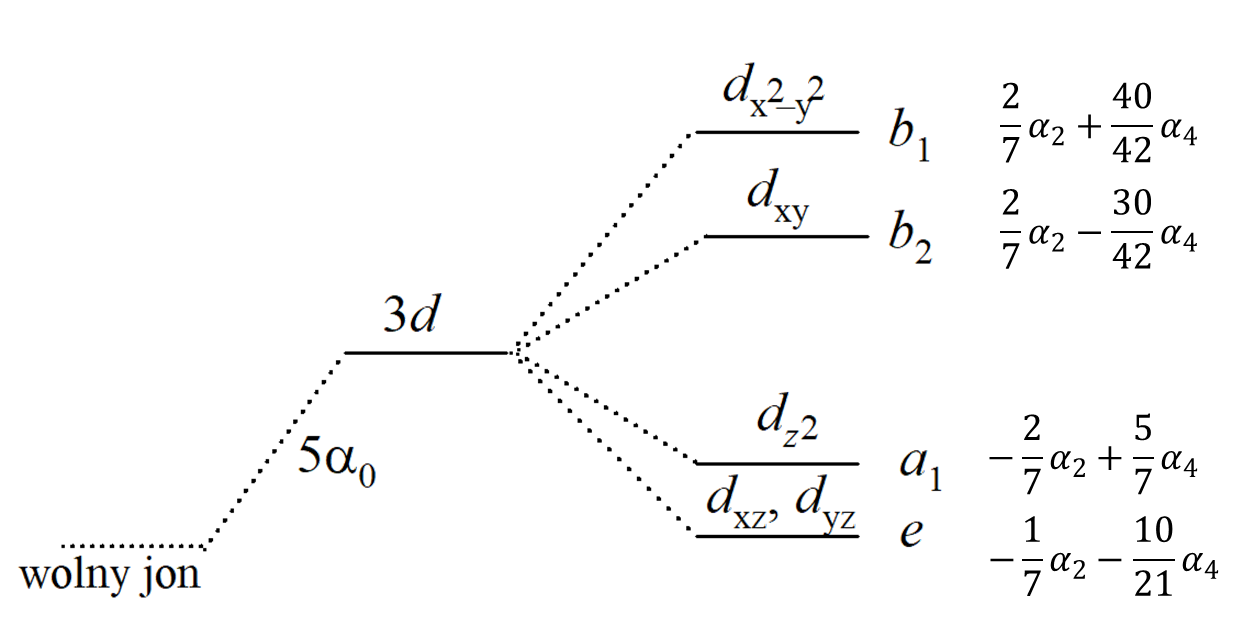Rozszczepienie w polu krystalicznym o symetrii C4v (piramida kwadratowa)

Rozważmy cząsteczkę ML₅ o geometrii bipiramidy trygonalnej. Oś główną (oś trójkrotna) oznaczymy jako z, i w takim razie jest ona wyraźnie różna od osi x i y znajdujących się w płaszczyźnie cząsteczki. W związku z tym orbital d_z² jest orbitalem wyróżnionym w stosunku do pozostałych czterech orbitali (a₁’ w grupie  D_3h). Wybierzmy jedno z wiązań metal–ligand w płaszczyźnie cząsteczki jako oś x; oś y w takim układzie staje się wektorem ułożonym pod kątem 90° do osi x, ale nie leży wzdłuż wiązania metal–ligand. Teraz względem tych osi można zdefiniować orbitale d_x2–y2 i d_xy. Teraz obróćmy cząsteczkę wokół osi z. Po obrocie nie można określić, które wiązanie metal–ligand znajdowało się na osi x (a zatem i na y). Nie jest też możliwe rozróżnienie, gdzie znajdowały się orbitale d_xy i d_x2–y2, dlatego muszą one reprezentować nierozróżnialną (zdegenerowaną) parę orbitali (e’ w D_3h) leżących w płaszczyźnie xy cząsteczki, a ponadto symetrycznych w stosunku do odbicia. Orbitale d_xz i d_yz mogą się różnić od dwóch rozpatrywanych wcześniej orbitali (e’), ponieważ d_xz i d_yz leżą powyżej i poniżej płaszczyzny xy cząsteczki. Jednak d_xz i d_yz nie mogą zostać rozróżnione między sobą, gdy, jak ma to miejsce w tym przypadku, x jest nieodróżnialne od y. W ten sposób orbitale d_xz i d_yz tworzą bazę dla dwuwymiarowej reprezentacji antysymetrycznej w odniesieniu do odbicia w płaszczyźnie xy, czyli e“ w D_3h.

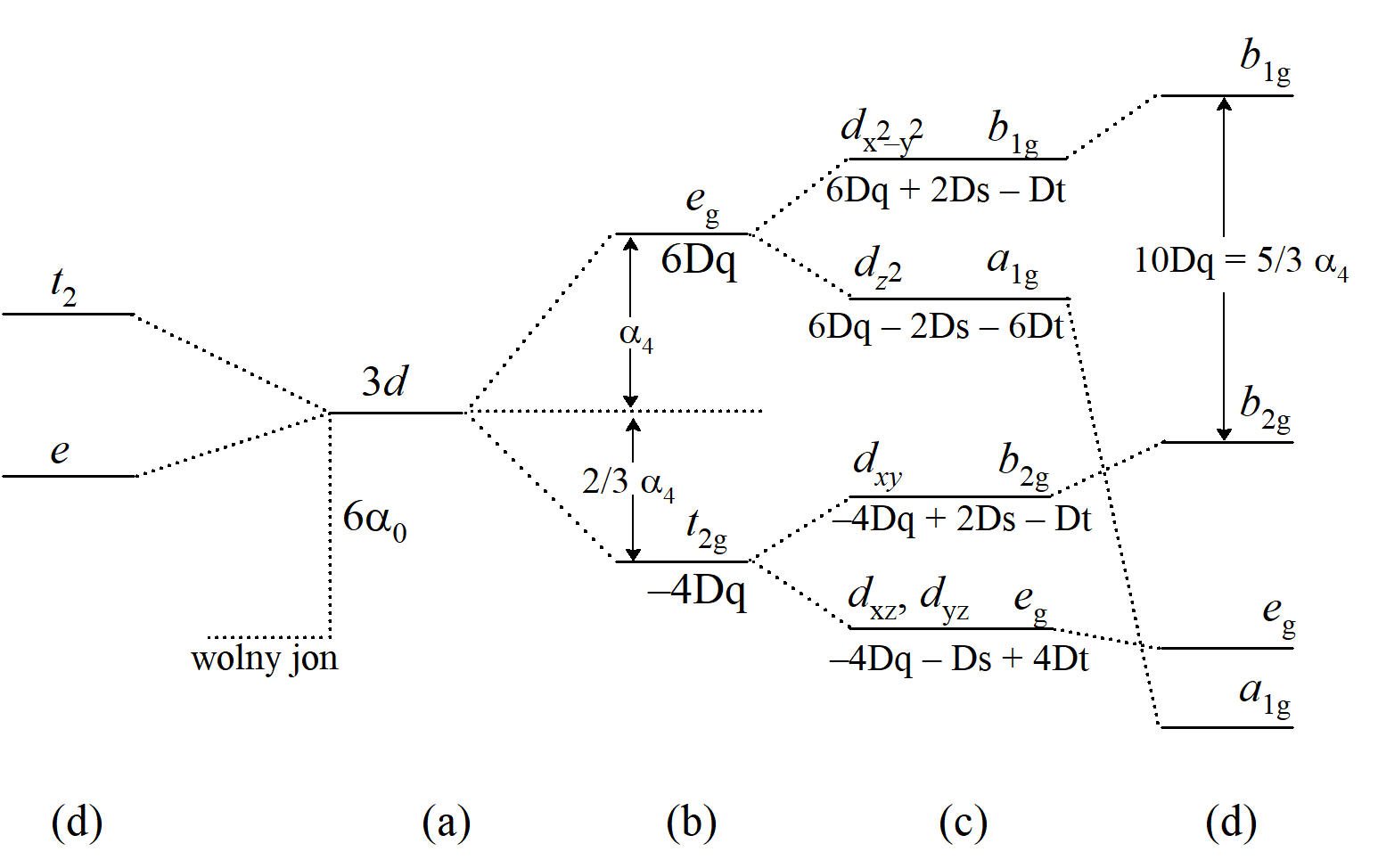Poziomy energetyczne: (a) sferycznie zaburzona powłoka d, (b) zaburzenie oktaedryczne, (c) oktaedr ze słabym odkształceniem tetragonalnym, (wydłużenie wzdłuż osi z), (d) silne zniekształcenie tetragonalne lub planarny układ kwadratowy, (e) zaburzenie tetraedryczne (sferyczny term 4a0).

Dlatego w trygonalnym bipiramidalnym polu symetrii, pięć orbitali d ulega rozdzieleniu na trzy poziomy, a₁', e' i e”. Ich względna kolejność jest mniej wyraźna, ale orbital d_z² ulegnie największej destabilizacji (leży przy najwyższej energii), ponieważ jest skierowany bezpośrednio na dwa ligandy. Orbitale w płaszczyźnie cząsteczki powinny być bardziej odpychane niż orbitale poza płaszczyzną, co prowadzi do sekwencji poziomów pokazanej na poprzednim rysunku. Ponieważ nie ma teoretycznego wymogu w grupie punktowej, aby wiązania metal–ligand w płaszczyźnie i poza płaszczyzną były równej długości (lub nawet, aby cząsteczka miała identyczne ligandy wzdłuż osi z i w płaszczyźnie xy), sekwencja pokazana na rys. 2 może się różnić w zależności od rozpatrywanej cząsteczki. Następnie orbitale e" powinny mieć bardzie zaznaczony charakter π-antywiążacy niż orbitale e', tak więc w kowalencyjnej cząsteczce, w której odgrywa rolę wiązanie p, kolejność poziomów może być odwrócona. Zauważmy jednak, że jeżeli symetria cząsteczki jest ściśle określona jako D_3h, orbitale d muszą rozdzielić się na orbitalny singlet i dwa orbitalne dublety.

Zastosujmy ten sam tok rozumowania do teragonalnego (D_4h) związku typu ML₄Z₂ (L leżą w płaszczyźnie xy, wszystkie kąty wynoszą 90°). Teraz ułożymy jedno wiązanie M–L na osi x, drugie na osi y, a jedno z wiązań M–Z na osi z. W związku z tym rozpatrując cząsteczkę nie ma problemu z określeniem osi z układu współrzędnych. Natomiast z perspektywy samej cząsteczki możemy jedynie stwierdzić, że x i y znajdują się w płaszczyźnie ML₄ rozpostartej na tych osiach, ale nie ma możliwości na ich jednoznaczne rozróżnienie. Na tej podstawie widzimy, że da się odróżnić d_z2 od d_x2–y2 i d_xy od d_xy, d_yz. W rozpatrywanym przypadku d_xy można odróżnić od d_x2–y2 (w przeciwieństwie do symetrii D_3h), ponieważ chociaż osi x nie można jednoznacznie zidentyfikować, wiadomo, że leży ona wzdłuż wiązania M–L. Zatem d_xy znajdujące się między wektorami wiązań jest odróżnialne od d_x2–y2 leżącego wzdłuż wiązań.

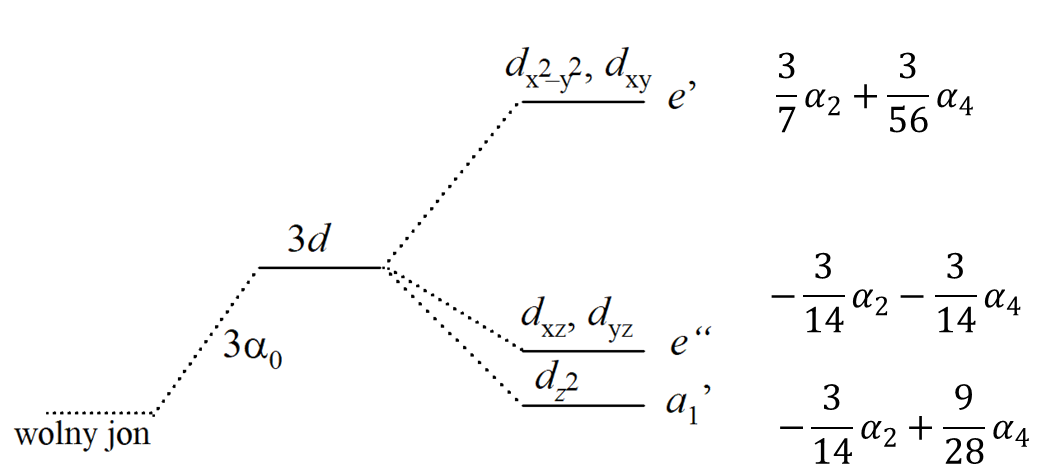Diagram rozszczepienia w polu o symetrii D3h (płaski trójkąt).

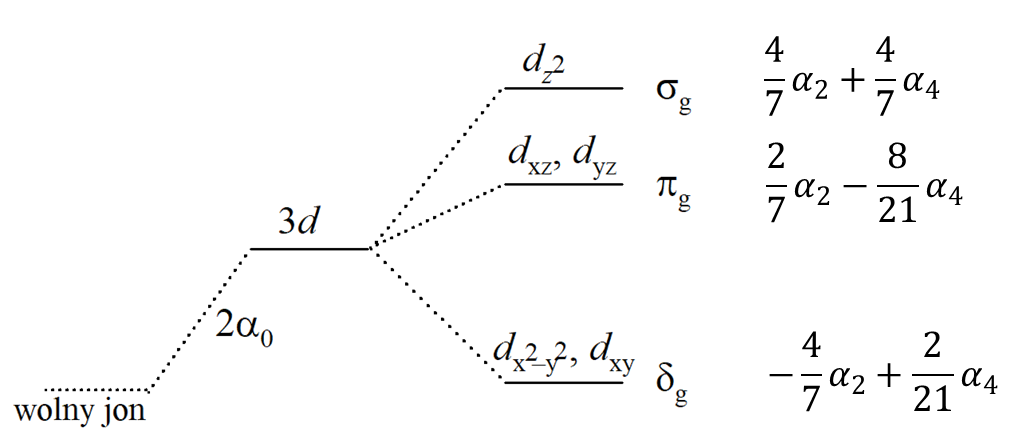Diagram rozszczepienia orbitali d dla cząsteczki liniowej.

Należy zwrócić uwagę, że skrajna prawa kolumna tabel charakterów grup zawiera reprezentacje dla różnych współrzędnych kartezjańskich i ich iloczynów. Iloczyny takie jak xy, xz itp., zachowują się tak samo pod względem symetrii, jak przekształcają się odpowiadające im orbitale d. Dlatego rozszczepienie orbitali d można wywnioskować rozważając prawą kolumnę tabeli charakterów dla danej grupy. Na przykład w grupie C_4v, odpowiedniej dla wielościanu o geometrii piramidy kwadratowej pięciokoordynacyjnego związku, xz, yz są nieodróżnialne i przekształcają się jako zdegenerowana reprezentacja e, podczas gdy pozostałe trzy orbitale mają różne energie, ponieważ przekształcają się jako trzy różne reprezentacje, a mianowicie xy jako b₂, x²–y² jako b₁ i z² jako a₁. Nic dziwnego, że charakter rozszczepienia dla pięciokoordynacyjnej cząsteczki o geometrii bipiramidy trygonalnej jest podobny do rozszczepienia dla trygonalnego płaskiego kompleksu o liczbie koordynacyjnej równej trzy, ale w tym drugim przypadku orbital d_z2 będzie najbardziej stabilny (najniższa energia).

Czterokoordynacyjne płaskie cząsteczki, pięciokoordynacyjne związki o geometrii piramidy o podstawie kwadratu oraz sześciokoordynacyjne związki typu ML₄Z₂ można wyprowadzić z oktaedru. W oktaedrze zamieniamy dwa ligandy L w pozycji trans na ligandy Z, o których zakładamy, że wywołują słabsze pole. Teraz oś z staje się wyróżniona, co powoduje utratę degeneracji d_z2 i d_x2–y2; podobnie xz, yz można teraz odróżnić od xy, co znosi degenerację dubletu i tripletu w oktaedrze. Natomiast całkowity ładunek wzdłuż osi określa energie orbitali d. Kompleks o pięciu ligandach z jednym ligandem Z o dwukrotnie większym natężeniu pola niż ten sam ligand w związku sześciokoordynacyjnym ML₄Z₂ miałby takie same energie orbitalne rozszczepionej podpowłoki d (należy pamiętać, że teoria pola krystalicznego operuje przybliżeniem jednoelektronowym, zaniedbując wzajemne oddziaływanie elektronów na orbitalach d). Zatem prawa strona poniższego diagramu jest również odpowiednia dla pięciokoordynacyjnych związków i pokazuje, zasadniczo, co się stanie, gdy natężenie pola wzdłuż osi z ulegnie zmniejszeniu (wydłużenie osiowe). Energia orbitalu d_x2–y2 rośnie wraz z obniżaniem się energii d_z2, ponieważ w rzeczywistej cząsteczce, gdy pole wzdłuż osi z maleje, dodatni ładunek pozostający na metalu wzrasta, co powoduje zwiększone przyciąganie ligandów w płaszczyźnie xy.

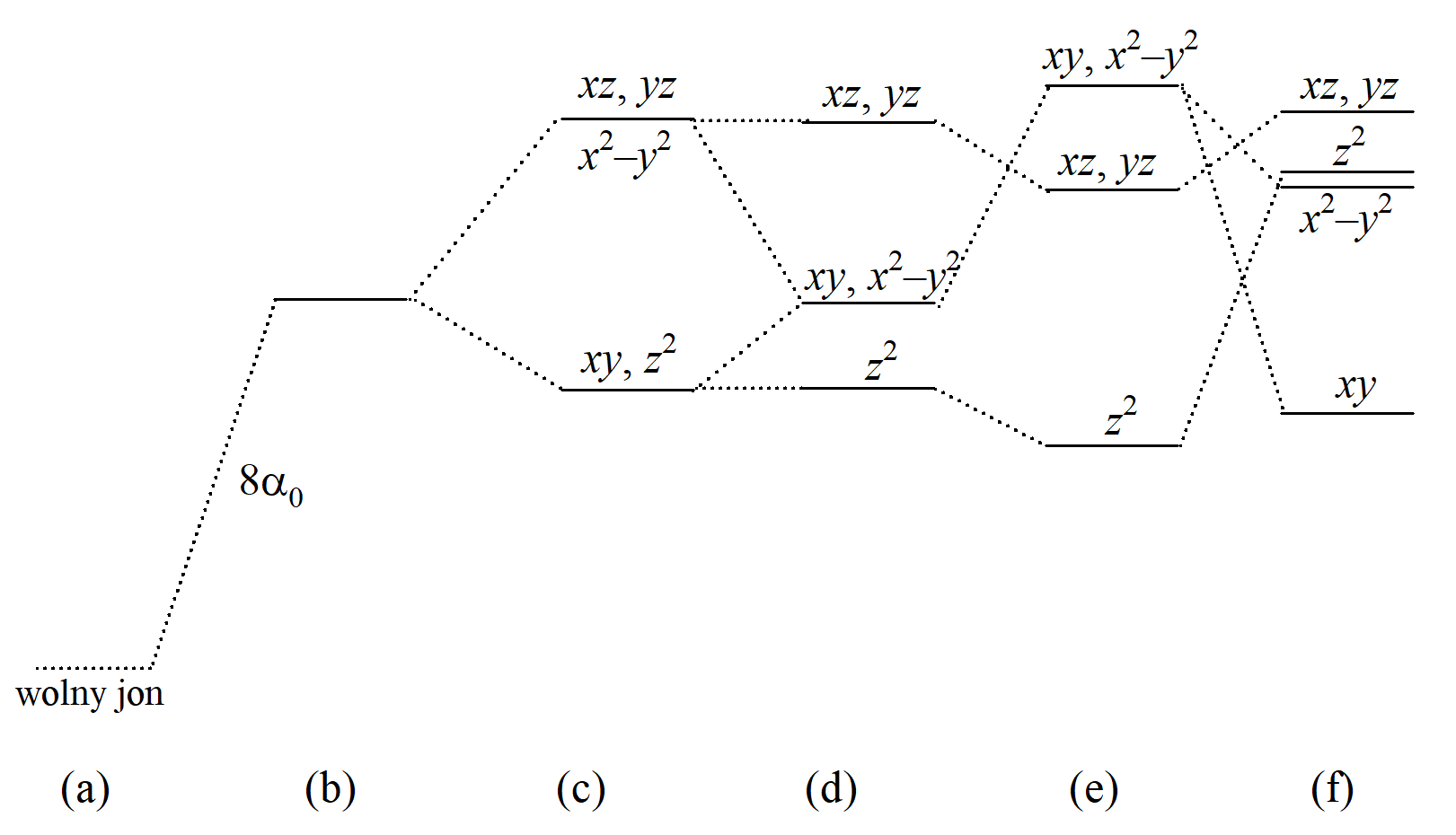Diagram rozszczepienia orbitali d w różnych polach ośmiokoordynacyjnych: (a) wolny jon, (b) sferycznie zaburzony poziom d, (c) sześcian (Oh), (d) sześcian zdeformowany tetragonalnie (D4d), (e) antypryzmat kwadratowy (D4d), (f) dodekaedr (D2d).

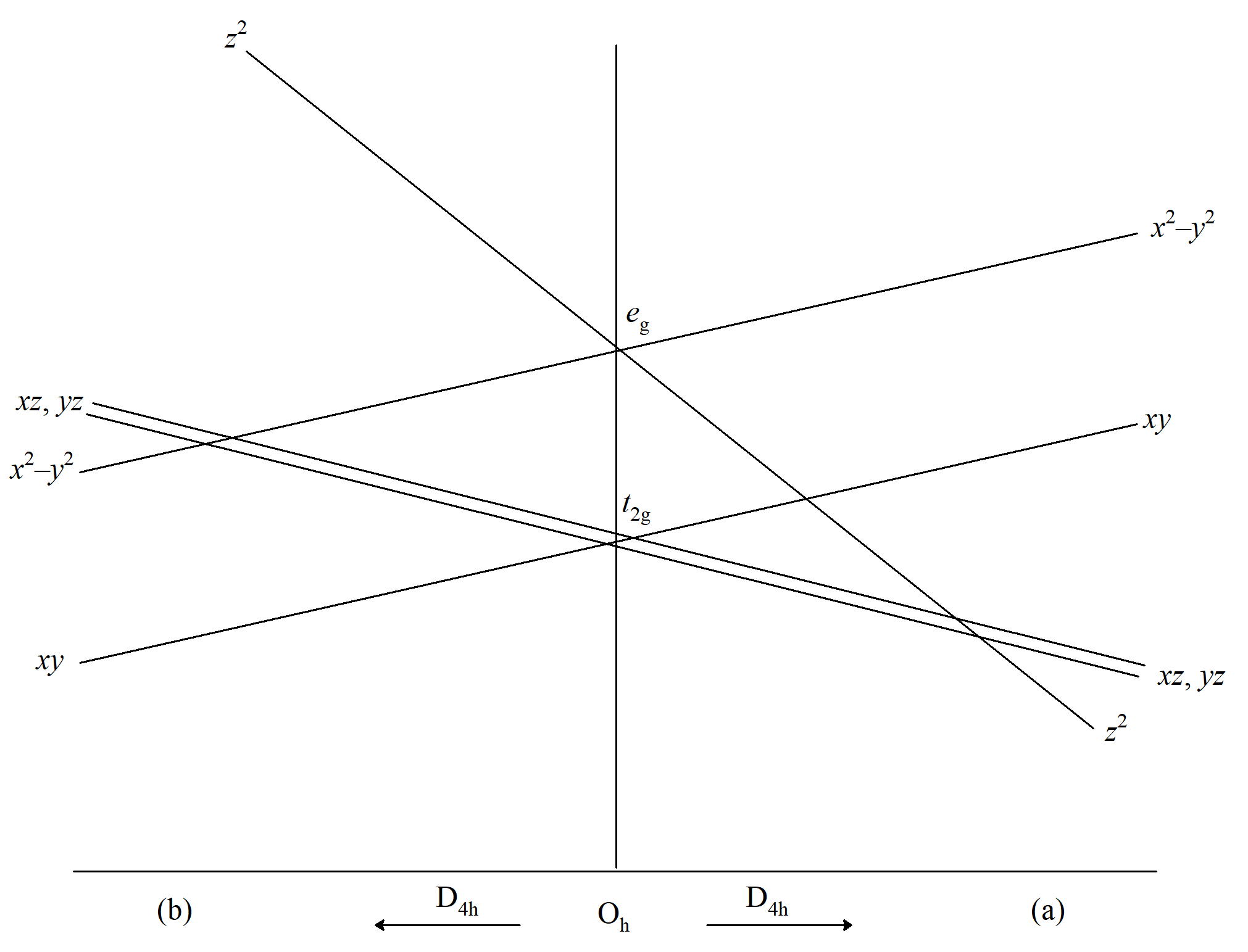Wpływ zniekształcenia tetragonalnego na poziomy energii w polu oktaedrycznym, (a) wydłużenie wzdłuż osi z; (b) wydłużenie w płaszczyźnie xy.

W granicy słabego pola wzdłuż osi z (braku pola) powstaje kwadratowa geometria planarna, której poziomy energetyczne znajdują się po skrajnej prawej stronie powyższego rysunku. Lewa strona odpowiada zbliżaniu się ligandów wzdłuż osi z, w którym pole wzdłuż tej osi  jest silniejsze niż pole w płaszczyźnie xy albo dlatego, że ligand Z wywiera silniejsze natężenie pola niż L, lub wiązanie M–Z jest krótsze niż wiązanie M–L. Granica zbliżania się ligandów wzdłuż osi zbiega się do cząsteczki liniowej. Jeśli ligandy w płaszczyźnie xy zostaną usunięte, orbitale d_xy i d_x2–y2 stają się zdegenerowane i powstanie diagram rozszczepienia dla cząsteczki liniowej.