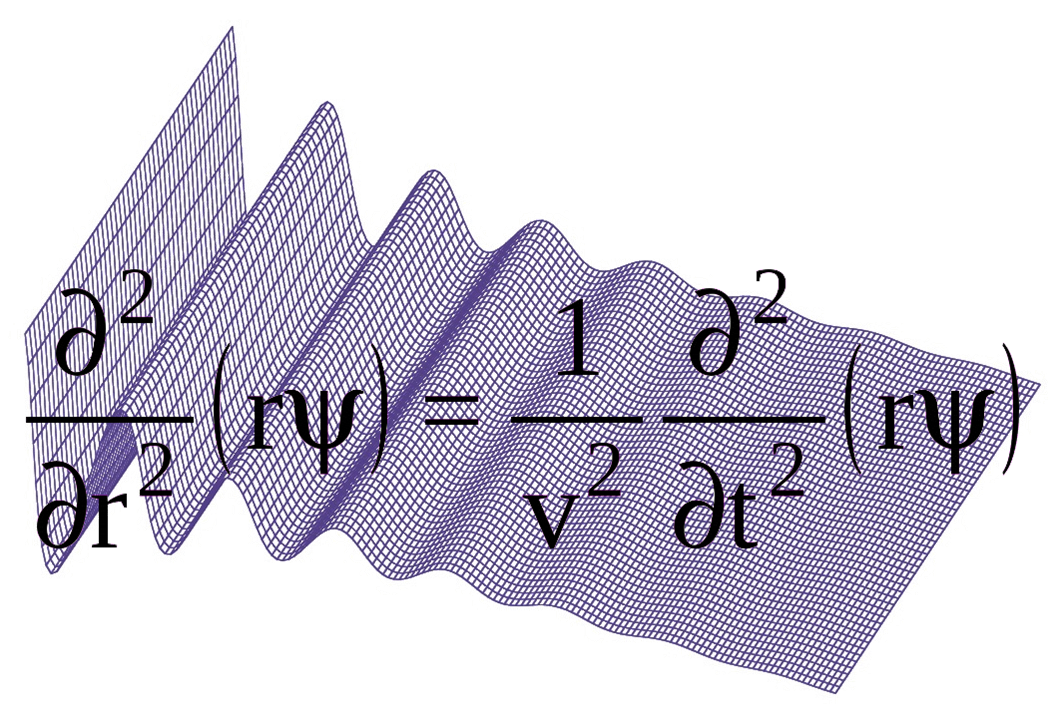Ruch w polu o symetrii sferycznej

W mechanice kwantowej, podobnie jak w mechanice klasycznej, problem ruchu dwóch cząstek można sprowadzić do zagadnienia ruchu jednej cząstki. Weźmy pod uwagę dwie cząstki o masach m₁ i m₂ oddziałujących ze sobą zgodnie z energią potencjalną U (r), gdzie r - oznacza odległość między cząstkami. Hamiltonian takiego układu ma postać:

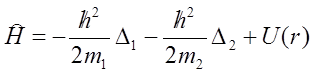gdzie Δ₁ i Δ₂ są operatorami Laplace’a, w których różniczkowanie dotyczy współrzędnych odpowiednio pierwszej i drugiej cząstki. Zdefiniujmy teraz dwie wartości:

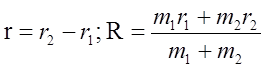r – oznacza wektor wzajemnej odległości pomiędzy cząstkami, a R promień wodzący środka masy cząstek. Teraz hamiltonian układu ma postać:

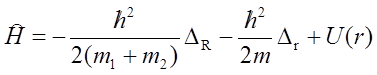gdzie Δ_R i Δ_r są operatorami Laplace’a odpowiednio względem wektorów R i r, m₁+ m₂ całkowitą masą układu, a m=m₁m₂/(m₁+ m₂) jest zredukowaną masa układu. Ponieważ hamiltonian rozpadł się na sumę dwóch niezależnych części to można szukać rozwiązania φ(r₁,r₂) w postaci iloczynu φ(R)φ(r), gdzie φ(R) opisuje ruch środka masy, φ(r) względny ruch cząstki jako ruch cząstki o masie m w polu centralnym U (r).

Równanie Schrödingera dla ruchu cząstki w polu centralnym ma postać:

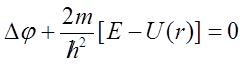 Rozpisując operator Laplace’a we współrzędnych sferycznych oraz wprowadzając operator kwadratu momentu pędu równanie to przyjmuje postać:

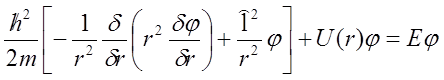Moment pędu jest stałą ruchu w polu centralnym, w związku z tym stany stacjonarne o określonym wartościach momentu pędu l i jego rzuty m określają zależność kontową funkcji falowej.. Czyli rozwiązania równania mają postać:

Funkcja własna momentu pędu spełnia równanie:

Po podstawieniu do równania Schrödingera otrzymujemy równanie dla funkcji radialnej R (r):

 Równanie to nie zawiera wartości l_z=m co odpowiada (2l+1)-krotnemu zdegenerowaniu poziomów ze względu na przestrzenne ustawienie momentu pędu. Wprowadźmy teraz zależność: R(r)=χ(r)/r otrzymując:

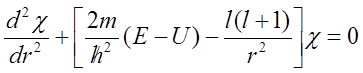 Zakładając, że energia potencjalna U (r) dąży do nieskończoności dla r→0 i czyni to wolniej niż 1/r ² czyli:

r ²U (r) → 0 dla r → 0

wykluczamy przypadek "spadnięcia" cząstki do środka pola. Przy takich warunkach funkcja falowa, a z nią gęstość prawdopodobieństwa |ψ|² jest skończona w całej przestrzeni łącznie z punktem r = 0. Jednocześnie funkcja χ=r R powinna być równa zero dla r =0. Dla danej dozwolonej wartości energii rozwiązanie równania Schrödingera przy warunku granicznym χ(0)=0 jest jednoznacznie określone , a przez to dla ruchu w polu centralnym stan układu w pełni określają wartości E, l, m czyli energia, wielkość i rzut momentu pędu. Dalej jeżeli ponumerujemy wartości własne energii widma dyskretnego o danym l liczbami n i przypiszemy najniższemu poziomowi numer 0, to kolejne numery określają liczbę węzłów radialnej części funkcji falowej dla skończonych wartości r, z wyłączeniem r = 0. Liczbę n nazywa się radialną liczbą kwantową, m zaś nosi nazwę magnetycznej liczby kwantowej. Stany o różnych wartościach momentu pędu l oznacza się symbolami:

Ruch w polu kulombowskim

Rozpatrzmy ruch elektronu w atomie wodoru lub jonie wodoropodobnym, czyli ruch elektronu w polu jądra o ładunku +Ze. Zakładamy nieruchomość jądra i wtedy zagadnienie sprowadza się do ruchu cząstki w polu przyciągania kulombowskiego:

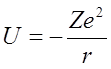Widmo poziomów energetycznych dodatnich wartości E będzie ciągłe, a ujemnych dyskretne, odpowiadające stanom związanym elektronu. W przypadku pola kulombowskiego wygodnie jest posługiwać się jednostkami atomowymi, przyjmując jako jednostki masy i długości odpowiednio masę elektronu i promień Bohra. Równanie dla funkcji radialnych w tych jednostkach ma postać:

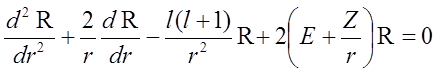Zamiast zmiennych E i r wprowadźmy:

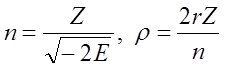gdzie n jest dodatnią liczbą rzeczywistą dla ujemnych wartości E. Wtedy równanie przyjmuje postać (’ i “ oznaczają pierwszą i drugą pochodną względem zmiennej ρ):

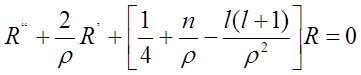Dla małych wartości ρ rozwiązanie spełniające warunek skończoności jest proporcjonalne do ρ^l. Natomiast asymptotyczną postać  funkcji R przy pominięciu dla dużych ρ wyrazów 1/ρ i 1/ρ² wyraża równanie:

R “=R/4

a stąd R = e^±ρ/2. Ponieważ interesuje nas rozwiązanie, które znika w nieskończoności, czyli dla dużych ρ ma ono postać e^–ρ/2. W związku z tym podstawmy do równania:

R = ρ^le^–ρ/2w(ρ)

i wtedy uzyskujemy równanie postaci:

ρw“ + (2l + 2 ~ ρ)w’ + (n – l – 1)w = 0

Równanie to powinno rozbieżne w nieskończoności, a dla ρ=0 powinno być skończone. Szukamy rozwiązania w postaci szeregu:

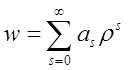Po podstawieniu do powyższego wzoru uzyskujemy:

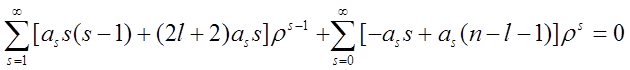lub po zmianie wskaźników sumowania z s na s+1:

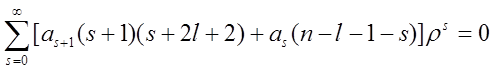Przyrównując do zera współczynniki rozwinięcia otrzymujemy związek rekurencyjny:

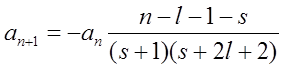Z tego wynika, że szereg w jest wielomianem stopnia n – l – 1 jeżeli n = l + 1, l + 2, ... . Zatem liczba n powinna być całkowita i dodatnia, przy czym dla każdego l :

n ≥ l +1

W ten sposób energia określona parametrem n dana jest wzorem:

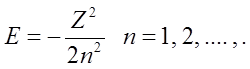Wzór ten określa nieskończony zbiór poziomów energetycznych widma dyskretnego energii w polu kulombowskim pomiędzy stanem podstawowym E₁= –1/2, a zerem. Poziomy energetyczne zagęszczają się wraz ze wzrostem n w miarę zbliżania się do E = 0, przy której widmo dyskretne przechodzi w widmo ciągłe. Przechodząc do zwykłych jednostek wzór na energię ma postać:

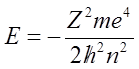Liczba n nosi nazwę głównej liczby kwantowej. Dla danej głównej liczby kwantowej liczba l przyjmuje wartości:

l = 0, 1, ..., n –1.

Ponieważ w wyrażeniu na energię występuje jedynie główna liczba kwantowa to stany o różnych l ale jednakowych n mają tę samą energię. W ten sposób każda wartość własna jest zdegenerowana nie tylko ze względu na magnetyczną liczbę kwantową m, lecz także ze względu na liczbę l. Ponieważ każdej wartości l odpowiada 2l + 1 stanów o wartości m, to stopień zwyrodnienia n-tego poziomu wynosi:

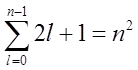W stanie podstawowym funkcja falowa ma postać:

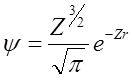i jest ona unormowana, czyli:

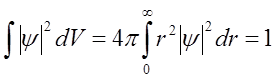"Rozmiary" atomu można scharakteryzować odległością r, dla której znacznie spada gęstość prawdopodobieństwa znalezienia elektronu |ψ|². Wielkość ta dla atomu wodoru Z=1 równa jest jednostce atomowej długości. W zwykłych jednostkach jest to promień Bohra a_B = ℏ²/me². Rząd wielkości prędkości elektronu w atomie określony jest zasadą nieoznaczoności: mv ~ ℏ/a_B , skąd v ~ e²/ℏ.