 Principles of Chemistry
Principles of Chemistry
- > Home
-
>
Historia chemii
- > Początki chemii
- > Rozwój alchemii
- > Jatrochemia
- > Badanie spalania i powietrza
- > Odkrycie i badanie gazów
- > Powstanie nowoczesnej chemii
- > Prawa chemiczne
- > Narodziny teorii atomowej
- > Elektrochemia
- > Berzelius, Hisinger, Faraday
- > Początki chemii organicznej
- > Substytucja
- > Wartościowość
- > Chemia fizyczna
- > Rozwój chemii nieorganicznej
- > Struktura atomu
-
>
Pierwiastki
- > Starożytność
- > Średniowiecze
- > Powietrze i woda
- > Analiza chemiczna
- > Halogeny
- > Elektrochemia
- > Metody spektroskopowe
- > Pierwiastki ziem rzadkich
- > Gazy szlachetne
- > Pierwiastki radioaktywne
- > Szeregi pierwiastków promieniotwórczych
- > Pierwiastki otrzymane sztucznie
- > Pierwiastki transuranowe
- > Podsumowanie
- > Układ okresowy
-
>
Mechanika falowa
- > Podstawy teoretyczne
- > Moment pędu
- > Równanie Schrodingera
- > Oscylator liniowy
- > Pole o symetrii sferycznej i pole kulombowskie
- > Spin
- > Identyczność cząstek
- > Oddziaływanie wymienne
- > Druga kwantyzacja
- > Poziomy energetyczne atomów
- > Układ okresowy
- > Atom w polu elektrycznym
- > Atom w polu magnetycznym
- > Cząsteczka dwuatomowa
- > Orto- i parawodór
- > Teoria relatywistyczna
- > Kwantowanie pola elektromagnetycznego
- > Fotony
- > Równanie Diraca
- > Cząstki i antycząstki
- > Atom i cząsteczka
-
>
Związki metali przejściowych
- > Powłoka walencyjna metali przejściowych
- > Efekt Jahna-Tellera
- > Teoria pola krystalicznego
- > Teoria pola ligandów
- > Widma elektronowe
- > Wiązania metal-metal
- > Własności magnetyczne
- > Trwałość związków koordynacyjnych
- > Związki z ligandami π–akceptorowymi
- > Arenowe związki koordynacyjne
- > Oddziaływania agostyczne
- > Wiązania chemiczne
- > Pojęcia chemii nieorganicznej
- > Mechanizmy reakcji
- > Oddziaływania międzycząsteczkowe
- > Elementy fizyki
- > Chemia organiczna
 Atom
Atom
Opierając się na zagadnieniach podanych poprzednio w zakładce Mechanika falowa, przejdziemy do opisu, na początek, najprostsze atomu , czyli atomu wodoru. Atom wodoru jest jedynym układem chemicznych, dla którego możliwe jest ścisłe rozwiązanie równania Schrödingera. Przy opisie atomu tego pierwiastka można wyjść od teorii Bohra, według której elektron obiega jądro (proton) po okręgu, którego promień wynosi a0. Wartość ta nosi nazwę promienia Bohra lub promienia pierwszej orbity Bohra. Promień ten jest związany z masą i ładunkiem elektronu wzorem:
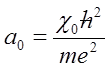 gdzie ℏ=h/2π, χ0=4πε0, a ε0 oznacza przenikalność elektryczną próżni.
gdzie ℏ=h/2π, χ0=4πε0, a ε0 oznacza przenikalność elektryczną próżni.
W mechanice falowej elektron w atomie wodoru opisuje funkcja falowa postaci:
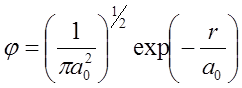 W wyrażeniu tym r oznacza odległość od początku układu. Gęstość prawdopodobieństwa wyznaczona podstawie funkcji falowej dana jest wzorem:
W wyrażeniu tym r oznacza odległość od początku układu. Gęstość prawdopodobieństwa wyznaczona podstawie funkcji falowej dana jest wzorem:
 Teraz ruch elektronu wokół jądra nie odbywa się już w płaszczyźnie, a w obszarze o symetrii kulistej. Prawdopodobieństwo znalezienia elektronu wewnątrz tego obszaru jest jednakowe we wszystkich punktach o takim samym r. Dodatkowo ponieważ obszar wyznaczony funkcją falową jest kulisty to funkcja ta jest unormowana.
Teraz ruch elektronu wokół jądra nie odbywa się już w płaszczyźnie, a w obszarze o symetrii kulistej. Prawdopodobieństwo znalezienia elektronu wewnątrz tego obszaru jest jednakowe we wszystkich punktach o takim samym r. Dodatkowo ponieważ obszar wyznaczony funkcją falową jest kulisty to funkcja ta jest unormowana.
Wynikiem takiego podejścia do atomu jest możliwość graficznego przedstawienia wykresu funkcji φ w zależności od r, a dodatkowo można przedstawić graficznie kontury stałych wartości tej funkcji lub prawdopodobieństwa znalezienia elektronu. Można również przedstawić chmurę ładunku w płaszczyźnie zaznaczając różne stopnie gęstości, jak również powierzchnię graniczną poza którą znajdzie się z góry ustalony niewielki ułamek całkowitego ładunku elektronu.
Funkcja falowa opisującą rozkład ładunku elektronu w atomie nosi nazwę orbitalu atomowego. Dla atomu wodoru w stanie podstawowym orbital ten ma kształt kuli, a maksymalna gęstość ładunku elektronu znajduje się w odległości a0 od jądra. Ponieważ mamy do czynienia z równaniami różniczkowymi to ten orbital jest tylko jednym z nieskończonej liczby rozwiązań równania Schrödingera dla atomu wodoru. Odpowiada on najniższej energii czyli stanowi podstawowemu atomu. Gdy atom zaabsorbuje energię wtedy nastąpi przejście do stanu wzbudzonego opisywanego orbitalem o wyższej energii.
Orbitale w atomach wieloelektronowych przedstawia się zazwyczaj jako funkcje zmiennych sferycznych r, θ, φ. Natomiast poglądowo łatwiej jest posługiwać się orbitalami atomowymi wyrażonymi we współrzędnych kartezjańskich. Wszystkie funkcje falowe jakie są dopuszczalne przy opisie atomów mają postać:
Ψnlm(r,θ,φ) = Rnl(r)Ylm(θ,φ).
Rozwiązania dla tych funkcji są zespołami wskaźników n, l, m, które to wskaźniki noszą nazwę liczb kwantowych. Liczby kwantowe przybierają wartości: n= 1, 2, 3 ..., l ≤ n–1, m = l, l–1, l–2, ..., –l. Liczba n określa energię i nosi nazwę głównej liczby kantowej. Gdy n > 1 to tej samej energii odpowiadają różne wartości l i m czyli różne stany elektronu w atomie. Zbiór tych stanów dla danej wartości energii nosi nazwę stanów zdegenerowanych, a ich liczba określa stopień degeneracji. Każdej wartości l odpowiada 2l+1 krotnie zdegenerowany stan odpowiednio do zbioru wartości liczby m. Przykładowo dla l =2 mamy trzy poziomy o wartościach liczby m równych odpowiednio 1, 0 i –1. Kolejne wartości liczby l oznaczane są literami s, p, d, f dla l = 0, 1, 2 3 . Oznaczenia literowe wywodzą się od angielskich nazw linii widmowych i tak s od słowa sharp (ostra), p – principal (główna), d – diffuse (rozmyta) i f – fundamental (podstawowa). Liczba kwantowa m nazywana jest magnetyczną liczbą kwantową, co również wywodzi się ze spektroskopii gdyż pole magnetyczne wpływa w różny sposób na stany o różnych wartościach m.
Nie wnikając w rozważania matematyczne kontury orbitali atomowych można przedstawić w następujący sposób:
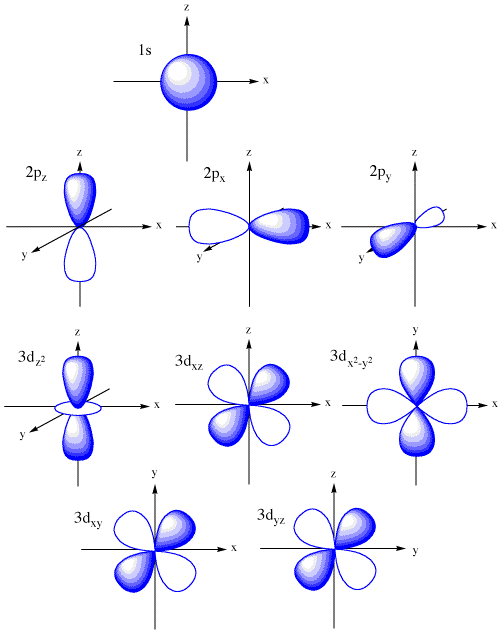
Dla wartości głównej liczby kwantowej n = 1występuje tylko jeden rodzaj orbitalu czyli orbital typu s. Dla n = 2 mamy orbital 2s oraz trzy, odpowiadające poszczególnym liczbom m, orbitale typu p. Orbitale te są skierowane wzdłuż osi układu kartezjańskiego i każdy z nich ma azymutalny węzeł w początku układu współrzędnych. Wszystkie trzy orbitale p, czyli px, py i pz mają tę samą energię czyli są trójkrotnie zdegenerowane. Degeneracja ta wynika z kulistej symetrii pola centralnego. Natomiast degeneracja orbitali 2s i 2p jest spowodowana szczególnymi właściwościami pola kulombowskiego, i nie wynika z symetrii. Dla n = 3 pojawia się trzeci rodzaj orbitali czyli orbitale d, które są pięciokrotnie zdegenerowane. Dla n równego 4 pojawia się kolejny rodzaj orbitali, są to orbitale f, z których siedem jest niezależnych.
 Dla atomów wieloelektronowych koncepcje zastosowane do opisu elektronu w atomie wodoru znajdują zastosowanie gdyż każdy elektron porusza się w pewnym sensie niezależnie od innych i można go opisać odpowiednim orbitalem. Inaczej mówiąc dla każdego elektronu możemy zapisać odpowiednie równanie falowe ale w przypadku atomu wieloelektronowego nie ma możliwości jego rozwiązania w sposób ścisły jak dla atomu wodoru. Wynika to z faktu, że ruch dowolnego elektronu w takim atomie jest uzależniony od ruchu wszystkich pozostałych elektronów. Ta nieseparowalność ruchów indywidualnych elektronów powoduje złożoność problemu. Rozwiązaniem jest założenie, że ruch każdego elektronu odbywa się w uśrednionym, efektywnym polu elektrycznym wynikającym z położeń wszystkich pozostałych elektronów w atomie. Takie podejście uzasadnia stosowanie funkcji falowych klasyfikowanych jako orbitale s, p, d i f, związanych z atomem wodoru. Ponieważ rozpatrujemy najniżej energetyczny stan atomu, to warunek ten określa odpowiednie wartości liczb kwantowych n, l, m a tym samym określonemu orbitalowi w myśl zasady Pauliego można przypisać tylko dwa elektrony różniące się wartością czwartej liczby kwantowej związanej ze spinem elektronu. W stanie podstawowym elektrony przypisujemy orbitalom 1s, 2s, 2p, i dalej 3s, 3p, 3d według wzrastającej energii tworząc konfigurację stanu podstawowego atomu. Ponieważ każdy z elektronów w atomie wieloelektronowym traktujemy jako odrębny, poruszający się w polu wszystkich pozostałych to skonstruowana w ten sposób funkcja falowa jest siłą rzeczy obarczona pewnym błędem. Jednak metoda taka pozwala na stopniowe uzyskanie, metoda kolejnych przybliżeń w miarę dokładnej funkcji falowej opisującej elektrony w takim atomie. Efektem zastosowanych przybliżeń jest uzyskanie opisu elektronu, który reprezentuje funkcja falowa, zwana orbitalem atomowym i mająca tę właściwość, że podobnie jak w atomie wodoru, jej kwadrat stanowi miarę gęstości związanej z elektronem chmury ładunku. Każdy z orbitali atomowych jest charakteryzowany układem liczb kwantowych, i elektrony o tej samej liczbie n należą do danej powłoki. Z każdym orbitalem atomowym związana jest pewna energia, wyznaczona z równania falowego i w przybliżeniu równa energii jonizacji Uszeregowanie orbitali względem ich energii można przedstawić następująco:
Dla atomów wieloelektronowych koncepcje zastosowane do opisu elektronu w atomie wodoru znajdują zastosowanie gdyż każdy elektron porusza się w pewnym sensie niezależnie od innych i można go opisać odpowiednim orbitalem. Inaczej mówiąc dla każdego elektronu możemy zapisać odpowiednie równanie falowe ale w przypadku atomu wieloelektronowego nie ma możliwości jego rozwiązania w sposób ścisły jak dla atomu wodoru. Wynika to z faktu, że ruch dowolnego elektronu w takim atomie jest uzależniony od ruchu wszystkich pozostałych elektronów. Ta nieseparowalność ruchów indywidualnych elektronów powoduje złożoność problemu. Rozwiązaniem jest założenie, że ruch każdego elektronu odbywa się w uśrednionym, efektywnym polu elektrycznym wynikającym z położeń wszystkich pozostałych elektronów w atomie. Takie podejście uzasadnia stosowanie funkcji falowych klasyfikowanych jako orbitale s, p, d i f, związanych z atomem wodoru. Ponieważ rozpatrujemy najniżej energetyczny stan atomu, to warunek ten określa odpowiednie wartości liczb kwantowych n, l, m a tym samym określonemu orbitalowi w myśl zasady Pauliego można przypisać tylko dwa elektrony różniące się wartością czwartej liczby kwantowej związanej ze spinem elektronu. W stanie podstawowym elektrony przypisujemy orbitalom 1s, 2s, 2p, i dalej 3s, 3p, 3d według wzrastającej energii tworząc konfigurację stanu podstawowego atomu. Ponieważ każdy z elektronów w atomie wieloelektronowym traktujemy jako odrębny, poruszający się w polu wszystkich pozostałych to skonstruowana w ten sposób funkcja falowa jest siłą rzeczy obarczona pewnym błędem. Jednak metoda taka pozwala na stopniowe uzyskanie, metoda kolejnych przybliżeń w miarę dokładnej funkcji falowej opisującej elektrony w takim atomie. Efektem zastosowanych przybliżeń jest uzyskanie opisu elektronu, który reprezentuje funkcja falowa, zwana orbitalem atomowym i mająca tę właściwość, że podobnie jak w atomie wodoru, jej kwadrat stanowi miarę gęstości związanej z elektronem chmury ładunku. Każdy z orbitali atomowych jest charakteryzowany układem liczb kwantowych, i elektrony o tej samej liczbie n należą do danej powłoki. Z każdym orbitalem atomowym związana jest pewna energia, wyznaczona z równania falowego i w przybliżeniu równa energii jonizacji Uszeregowanie orbitali względem ich energii można przedstawić następująco:
 W atomie wieloelektronowym degeneracja orbitali o różnej symetrii, pochodzących z tej samej powłoki zostaje zniesiona. Energia atomu jest równa sumie energii poszczególnych elektronów z uwzględnieniem poprawki związanej z oddziaływanie elektronów.
W atomie wieloelektronowym degeneracja orbitali o różnej symetrii, pochodzących z tej samej powłoki zostaje zniesiona. Energia atomu jest równa sumie energii poszczególnych elektronów z uwzględnieniem poprawki związanej z oddziaływanie elektronów.
Przypisując elektrony do orbitali należy kierować się zakazem Pauliego, zgodnie z którym żaden z orbitali nie może zawierać więcej niż dwóch elektronów, które muszą na danym orbitalu mieć przeciwne spiny. Kolejną regułą jaka obowiązuje przy zapełnianiu orbitali elektronami jest reguła Hunda, zgodnie z którą obsadzanie elektronami orbitali zdegenerowanych wykonuje się zachowując maksymalną liczbę elektronów niesparowanych. Zasady zapełniania elektronami orbitali atomowych jednoznacznie wyjaśniają strukturę układu okresowego pierwiastków. Dwa elektrony na orbitalu 1s2 wypełniają całkowicie powłokę K, osiem elektronów na orbitalach 2s22p6 tworzy powłokę L itd. Dodatkowo z teorii wynika, że promień atomu zależy od liczby elektronów i ładunku jądra. Zgodnie z tym zwiększaniu ładunku jądra odpowiada "kurczenie się" promienia atomowego. Dlatego gazy szlachetne mają najmniejsze promienie atomowe, a metale alkaliczne największe. Elektrony walencyjne w atomach pierwiastków pierwszej grupy rozpoczynają zapełnianie orbitali kolejnej powłoki, którą kończą elektrony atomów gazów szlachetnych.
Termy – stany energetyczne w atomie
Rozpatrując atom zamkniętopowłokowy, taki jak atom helu czy berylu, stosując przybliżenie jednoelektronowe możemy bez trudu określić jego konfigurację, ponieważ istnieje tylko jeden sposób przypisania elektronów do odpowiednich orbitali spinowych (jednoelektronowych). Inaczej sytuacja wygląda w przypadku atomów otwartopowłokowych. Weźmy pod uwagę konfigurację podstawową atomu azotu N: 1s2 2s2 2p3. Na podpowłoce 2p mamy sześć orbitali spinowych (2pxα, 2pxβ, 2pyα, 2pyβ, 2pzα, 2pzβ), na których mamy do rozlokowania 3 elektrony. W pierwszym przybliżeniu każdy ze sposobów rozlokowania elektronów na orbitalach p będzie miał taką samą energię czyli mamy do czynienia ze stanem zdegenerowanym. Jednak jeżeli uwzględnimy oddziaływanie elektronów ze sobą otrzymamy poziomy o różnej energii odpowiadające stanowi faktycznemu obserwowanemu na drodze eksperymentalnej. Konkretne poziomy energetyczne charakteryzujące się określonymi wartościami liczb kwantowych noszą nazwę termów atomowych. Jak widać określonej konfiguracji elektronowej atomu może odpowiadać kilka termów różniących się energią. Charakterystyka termów czyli stanów elektronowych atomu wymaga określenia dla nich wartości własnych operatorów kwadratu momentu pędu i kwadratu spinu lub liczb kwantowych określających te wartości własne. Dla atomu wieloelektrodowego mamy zbiór liczb L, S, ML i Ms, odpowiadających liczbom kwantowym dla atomu wodoru. Skoro tak, to jeżeli wypadkowy moment pędu wszystkich elektronów wynosi L, to odpowiadająca mu liczba ML przyjmuje wartości od –L do L, czyli stan jest zdegenerowany (2L+1) krotnie. Podobnie dla spinu mamy (2S+1) krotną degenerację nazywaną multipletowością. Oznaczenia termów są analogiczne jak w przypadku stanów jednoelektrodowych, i tak dla L = 0, 1, 2, 3 itd. stosuje się symbole S, P, D, F i dalsze z pominięciem litery J. Po lewej stronie symbolu termu, u góry, podaje się jego multipletowość.
Mamy jeszcze jedną wartość różnicującą termy, a jest nią całkowity moment pędu elektronów będący wektorową sumą orbitalnego i spinowego momentu pędu. Dla oznaczenia tej wartości stosuje się literę J gdy dotyczy ona wszystkich elektronów w atomie lub j gdy stosujemy ją do jednego elektronu. W związku z tym termy opisuje się za pomocą ogólnego symbolu: 2S+1LJ. Ponieważ całkowity moment pędu jest sumą wektorową to przyjmuje on wartości w zakresie L+S do │L–S│czyli 2S+1 różnych wartości, gdy S ≤ L lub 2L+1 gdy L < S.
Dla zamkniętopowłokowych atomów stanem (termem) podstawowym jest term 1S, ponieważ dla elektronów tworzących zamkniętą powłokę (lub podpowłokę) wypadkowy orbitalny moment pędu i wypadkowy spin są zawsze równe zeru. Weźmy pod uwagę atom boru mający jeden elektron na orbitalu p. Spin tego elektronu wynosi ½, a rzut orbitalnego momentu pędu może być równy +1, 0, –1 w zależności od tego, który z orbitali p zajmuje elektron. Z tego wynika, że całkowity orbitalny moment pędu wynosi 1 i podstawowym stanem jest term 3P. W przypadku, gdy na orbitalu p znajdują się dwa elektrony sytuacja staje się bardziej skomplikowana, ale biorąc pod uwagę wartości ML i MS dla poszczególnych przyporządkowań elektronów możemy dla konfiguracji p 2 określić trzy termy: 1D, 3P i 1S. Aby określić term podstawowy posługujemy się regułami Hunda, zgodnie z którymi:
- termem podstawowym jest term o największej multipletowości;
- spośród termów o największej multipletowości termem podstawowym jest term o największej wartości L;
- jeżeli podpowłoka jest zapełniona elektronami mniej niż w połowie to poziomem podstawowym jest poziom o najmniejszej wartości J; jeśli podpowłoka zapełniona jest więcej niż w połowie to jest nim term o najwyższej wartości J.
W związku z tym schemat rozszczepienia termów dla konfiguracji elektronowej p 2 można przedstawić następującym schematem.
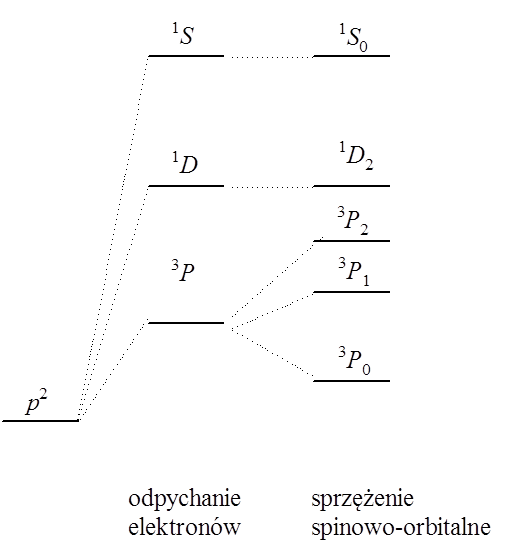 Termy podstawowe dla poszczególnych konfiguracji podpowłok p i d są następujące:
Termy podstawowe dla poszczególnych konfiguracji podpowłok p i d są następujące:
|
konfiguracja |
Termy |
|
p1, p5 |
2P |
|
p2, p4 |
3P, 1D, 1S |
|
p3 |
4S, 2D, 2P |
|
d 1, d 9 |
2D |
|
d 2, d 8 |
3F, 3P, 1G, 1D, 1S |
|
d 3, d 7 |
4F, 4P, 2H,2G,2F, 2D(2), 2P |
|
d 4, d 6 |
5D, 3H, 3G,3F(2),3D, 3P(2), 1I, 1G(2), 1F, 1D(2), 1S(2) |
|
d 5 |
6S, 4G, 4F, 4D, 4P, 2I, 2H, 2G(2), 2F(2), 2D(3), 2P, 2S |
W związkach koordynacyjnych wykazano, że dla układów oktaedrycznych, tetraedrycznych i sześciennych termy jonu centralnego niezależnie od multipletowości rozszczepiają się na:
S → A1 (singletowy)
P → T1 (tripletowy)
D → E (dubletowy) + T2 (tripletowy)
F → A2 (singletowy) + T1 (tripletowy) + T2 (tripletowy)
G → A1 (singletowy) + E (dubletowy) + T1 (tripletowy) + T2 (tripletowy)
Dla układów, w których sprzężenie Russella–Saundersa odgrywa rolę, wystarcza niewielka liczba parametrów opisujących różnice pomiędzy termami. Dla podpowłoki d opis zróżnicowania termów umożliwia zastosowanie trzech parametrów, a dla orbitali f – czterech. Mowa tu o parametrach Racah. Energię termów można więc wyrazić za pomocą całek Slatera–Condona (F0, F2, F4) lub prościej za pomocą parametrów A, B i C. Związek pomiędzy tymi dwoma formalizmami jest następujący:
A= F0 – 49F4; B= F2 – 5F4; C=35F4
W związku z tym energię termów dla podpowłoki d można wyrazić poprzez parametry Racah w sposób następujący:
| d2, d8 |
3F = A – 8B 3P = A + 7B 1G = A + 4B + 2C 1D = A – 3B +2C 1S = A + 14B +7C |
| d3, d7 |
4F = 3A – 15B 4P = 3A 2H = 3A – 6B + 3C 2G = 3A – 11B + 3C 2F = 3A + 9B + 3C 2D(2) = 3A + 5B + 5C ± (193B2 + 8BC + 4C2)½ |
| d4, d6 |
5D = 6A – 21B 3H = 6A – 17B + 4C 3G = 6A – 12B +4C 3F = 6A – 5B +11/2C ± (68B2 + 4BC + 9C2)½ 3D = 6A – 5B + 4C 3P = 6A – 5B +11/2C ± ½ (912B2 – 24BC +9C2)½ 1I = 6A –15B + 6C 1G = 6A – 5B + 15/2C ± 0.5(708B2 – 12BC + 9C2)½ 1F = 6A + 6C 1D = 6A + 9B + 15/2C ± 3/2(144B2 + 8BC + C2)½ 1S = 6A + 10B + 10C ± 2(193B2 + 8BC + 4C2)½ |
| d5 |
6S = 10A – 35B 4G = 10A – 25B + 5C 4F = 10A – 13B + 7C 4D = 10A – 18B + 5C 4P = 10A – 28B + 7C 2I = 10A – 24B + 8C 2H = 10A – 22B + 10C 2G = 10A – 13B + 8C 2G = 10A + 3B + 10C 2F = 10A – 9B + 8C 2F = 10A – 25B + 8C 2D = 10A – 4B + 10C 2D = 10A – 3B + 11C ± 3(57B2 + 2BC + C2) ½ 2P = 10A + 20B + 10C 2S = 10A – 3B + 8C |
Zapis energii termów przy użyciu parametrów Racah jest wykorzystywany nie tylko do opisu elektronów w atomach, lecz również ma odniesienie do opisu struktur elektronowych związków koordynacyjnych.