Termodynamika statystyczna

Warunkiem równowagi termodynamicznej układu w stałej objętości i energii jest aby entropia układu znajdowała się w maksimum. Z drugiej strony wiadomo, że najprawdopodobniejszy stan makro to taki któremu odpowiada maksymalna liczba stanów mikro. Zatem istnieje związek pomiędzy entropią S, a liczba stanów mikro realizujących dany stan makroskopowy L. Liczbę stanów miro nazywamy prawdopodobieństwem termodynamicznym, a entropię możemy zapisać w postaci funkcji prawdopodobieństwa termodynamicznego:

S = f(L)

Entropia, jak wiadomo, jest wielkością addytywną. Gdy jeden z układów ma entropię równą S₁, a drugi S₂, to entropia układu złożonego z nich dwóch wyniesie:

S_1,2 = S₁ + S₂

Natomiast prawdopodobieństwo termodynamiczne układu obejmującego układy 1 i 2 będzie równe, zgodnie z zasadami rachunku prawdopodobieństwa, iloczynowi prawdopodobieństw L₁L₂.  W związku z tym mamy spełnione równania:

f(L₁) = S₁

f(L₂) = S₂

f(L₁L₂) = L₁·L₂

czyli:

f(L₁L₂)= f(L₁) + f(L₂)

Z tego wynika, że funkcja wyrażająca zależność entropii od prawdopodobieństwa termodynamicznego musi być funkcją logarytmiczną. Zatem można zapisać:

S = c·lnL + a,

gdzie c i a są pewnymi stałymi. 

Jako postulat termodynamiki statystycznej przyjmuje się za Planckiem, że pomiędzy entropią a prawdopodobieństwem termodynamicznym zachodzi zależność:

S = k·lnL

czyli stała c jest równa stałej Boltzmanna, a wielkość a jest równa 0. W przypadku układów kwantowych podlegających statystyce kwantowej równanie to jest spełnione gdy prawdopodobieństwo stanów makro jest równe liczbie możliwych stanów kwantowomechanicznych. W dalszej części zajmiemy się gazem doskonałym czyli układem cząstek nie oddziałujących ze sobą.

W statystyce Bosego-Einsteina, czyli dla bozonów, liczba stanów kwantowomechanicznych układu złożonego z N cząstek dana jest wyrażeniem:

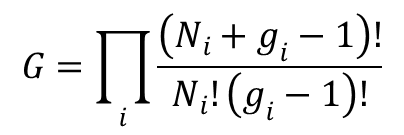
Po zlogarytmowaniu i przekształceniu otrzymujemy:

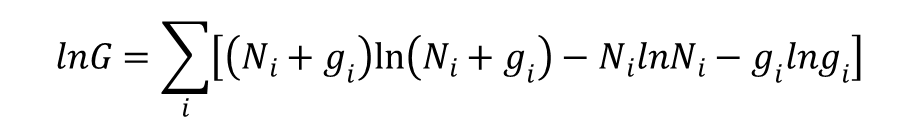
lub:

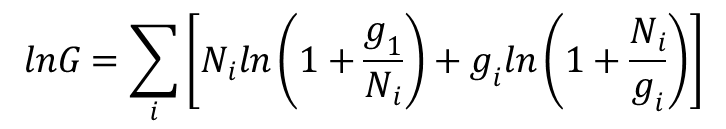
W normalnych warunkach ciśnienia i temperatury spełniony jest dla atomów i cząsteczek warunek przechodzenia statystyk kwantowych w formę klasyczną:

Wówczas otrzymujemy dla bozonów równanie:

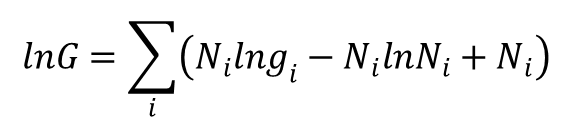
Dal fermionów, rządzonych statystyką Fermiego-Diraca, liczba stanów kwantowych układu złożonego z N cząstek określona jest wyrażeniem:

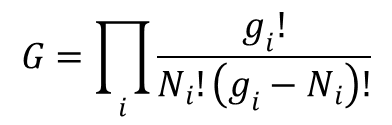
Po zlogarytmowaniu i zastosowaniu wzoru Stirlinga otrzymujemy:

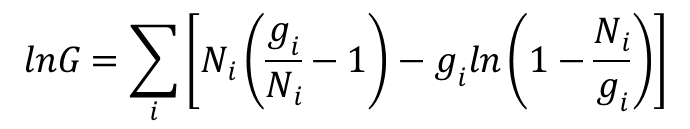
W normalnych warunkach fizykochemicznych, gdy  , otrzymujemy zaprezentowane powyżej równanie. Czyli dla bozonów i fermionów w zwykłych warunkach obowiązuje to samo równanie opisujące prawdopodobieństwo termodynamiczne. Zatem entropię możemy wyrazić równaniem:

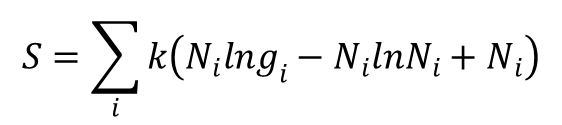
Ponieważ w warunkach normalnych statystyki kwantowe przechodzą, dla atomów i cząsteczek, w statystykę klasyczną, to można do opisu stanu najbardziej prawdopodobnego (stanu równowagi) zastosować rozkład Maxwella i Boltzmanna, w ogólnej formie:

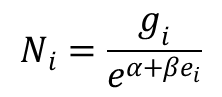
Po zlogarytmowaniu dostajemy:

lng_i = lnN_i + α + βe_i

a wzory na entropię mają postać:

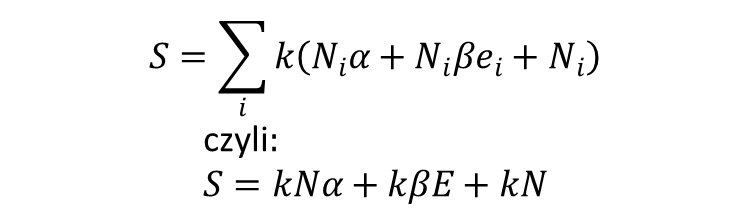
gdzie:

 

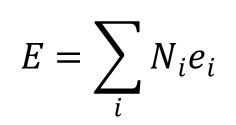
oznacza całkowitą energię N cząstek. ponieważ β = 1/kT można powyższe równanie na entropię zapisać w postaci:

Ponieważ N_i = g_ie^–α·e^–βe_i, to po obustronnym sumowaniu na wszystkie i otrzymujemy:

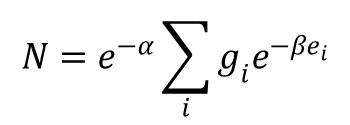a stąd:

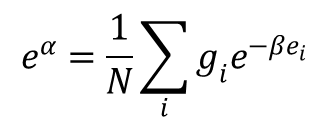
 Oznaczmy sumę występującą w ostatnim równaniu literą f:

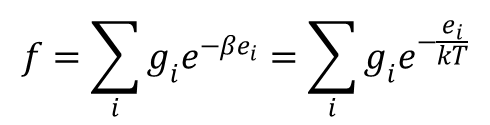
otrzymamy wyrażenie

e^α = f/N

skąd α = ln(f / N). Tym samym wyrażenie na entropię gazu w stanie równowagi przyjmuje postać:

Podstawowe wzory termodynamiki statystycznej na funkcje termodynamiczne dla gazu doskonałego w stanie równowagi

Z definicji entalpi swobodnej G = E + pV – TS. Podstawiając wyznaczoną powyżej entropię do tego wzoru otrzymujemy:

ponieważ dla gazu doskonałego pV = NkT, otrzymujemy równanie:

Oznaczając funkcję Helmholtza U – TS literą F = G – pV otrzymujemy:

Stosując wyrażenie na entropię dane wzorem:

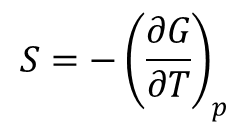otrzymujemy dla gazu doskonałego:

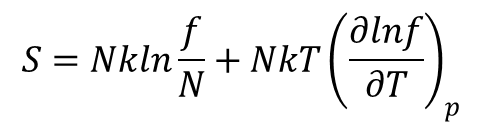
 Natomiast wychodząc z równania:

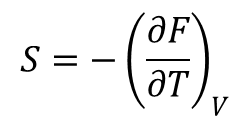
otrzymujemy:

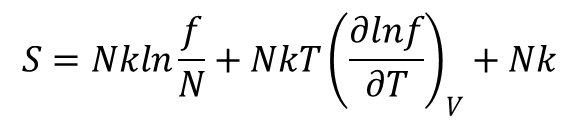
Kolejne dwa równania dla gazu doskonałego:

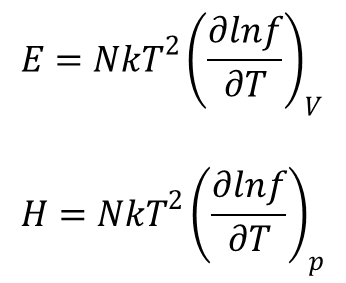
Wyrażają funkcje termodynamiczne za pomocą funkcji f lub jej pierwszych pochodnych po temperaturze.

Funkcja rozdziału

Zasadniczą rolę w przedstawionych powyżej równaniach termodynamiki statystycznej odgrywa funkcja f dana wzorem:

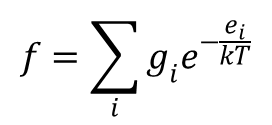
Funkcja ta nosi nazwę sumy stanów lub funkcji rozdziału. Wielkości e_i oznaczają w niej poszczególne poziomy energetyczne cząstki, a g_i odpowiadające tym poziomom liczby stanów kwantowomechanicznych, a tym samym wagi tych poziomów. Istotnym zagadnieniem przy rozpatrywaniu funkcji podziału jest ustalenie poziomu zerowego, od którego będzie się liczyło poziomy energetyczne cząsteczki. Musimy zdawać sobie sprawę, że doświadczalnie mierzymy tylko zmiany energii a niej wartość bezwzględną. Inaczej mówiąc w wyznaczonej wartości energii zawsze jest zawarty udział pewnego umownego poziomu zerowego. Ponieważ poziom zerowy jest zawsze umowny to zastanówmy się w jakim stopniu wpływa on na  funkcję f, a tym samym na funkcje termodynamiczne.

Przyjmijmy, że mamy gaz doskonały złożony z N cząstek, a wartość funkcji rozdziału obliczona przy uwzględnieniu poziomu zerowego wynosi f. Teraz przesuńmy poziom zerowy o pewną wartość ε₀. Energia cząstki w takim wypadku wyniesie e’=e_i + ε₀. W takim wypadku funkcja rozdziału przyjmuje postać:

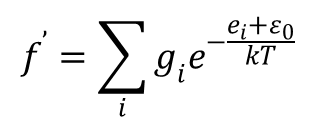
gdzie e_i oznacza energię cząstki liczoną od pierwotnego poziomu zerowego. Równanie to można zapisać w formie:

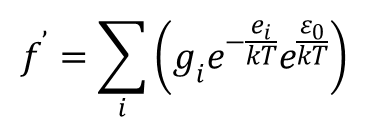
czyli

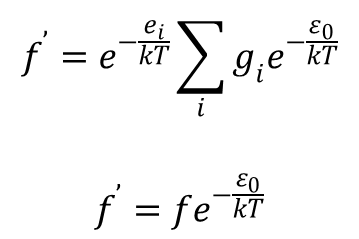
Z tego wynika, że:

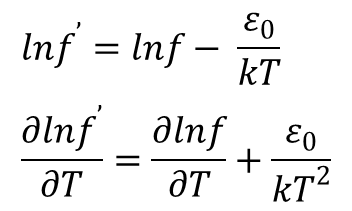
Stąd otrzymujemy:

G’ = G + N<ε₀

F’ = F + Nε₀

E’ = E + Nε₀

H’ = H + Nε₀

S’ = S

Zatem przesunięcie umownego poziomu zerowego energii cząsteczki o pewną wartość ε₀ powoduje zmianę funkcji rozdziału, wyrażającą się w przemnożeniu jej przez czynnik exp(–ε₀/kT), oraz zmianę energii wewnętrznej, entalpii, energii swobodnej i entalpii swobodnej układu wyrażającej się dodaniem czynnika Nε₀. Natomiast nie wpływa na wartość entropii.

Istotnym jest, że ogólna funkcja rozdziału dla danej cząstki daje się rozłożyć na iloczyn funkcji rozdziału dla poszczególnych postaci energii cząstki. Często przyjmuje się, że energia cząstki składa się addytywnie z energii translacyjnej oraz pozostałych form energii określanych jako energia wewnętrzna. Energię wewnętrzną dzieli się na energię rotacyjną, oscylacyjną i elektronową. Do funkcji rozdziału wchodzi jeszcze czynnik g_j związany ze spinem jąder cząstki. Czynnik ten wyraża liczbę różnych stanów kwantowych wywodzących się ze spinu cząstki, zwiększając g_j krotnie ogólną liczbę stanów kwantowych cząstki. W takim wypadku funkcja rozdziału ma ogólną postać:

f =f_trf_rotf_oscf_elg_j

Rzędy wielkości poszczególnych składowych funkcji rozdziału dla cząsteczki dwuatomowej można oszacować następująco. Funkcja rozdziału energii oscylacyjnej to około 1; energii rotacyjnej 10² – 10³; energii translacyjnej 10²⁵ – 10³⁰; energii elektronowej około 1.

Wyrażenia na poszczególne funkcje rozkładu dla gazu doskonałego

Energia translacji:

m - masa cząstki; V objętość gazu

Energia rotacji:

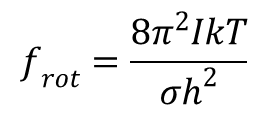
gdzie I oznacza moment bezwładności; σ - liczba symetrii cząsteczki oznaczająca ile razy w ciągu jednego pełnego obrotu zajmuje ona w przestrzeni identyczne położenie. Dla nieliniowych cząsteczek wieloatomowych funkcja rozdziału energii rotacji przyjmuje postać:

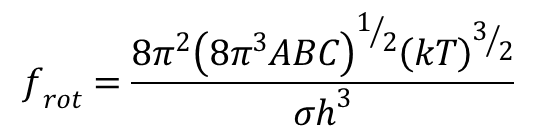
gdzie A, B i C oznaczają momenty bezwładności względem trzech osi obrotu.

Energia oscylacji:/p>

dla cząsteczki dwuatomowej

gdzie ν_osc oznacza częstość oscylacji.

Dla cząsteczek wieloatomowych jest iloczynem funkcji rozdziału dla każdej z oscylacji z osobna:

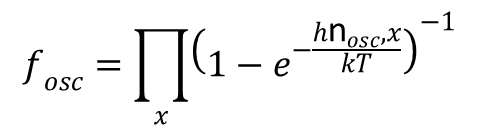
Energia elektronowa

Dal atomów liczba j w termie stanu podstawowego atomu wynosi j₀, w termie pierwszego stanu wzbudzonego j₁, drugiego stanu wzbudzonego j₂ itd. Kwant odpowiadający przejściu ze stanu podstawowego do pierwszego stanu wzbudzonego ma energię hν₁, do drugiego stanu wzbudzonego hν₂ itd. Jako punkt zerowy przyjmujemy energię w elektronowym stanie podstawowym.

W przypadku cząsteczek stan podstawowy ma charakter ¹Σ a  stany wzbudzone są z reguły wysoko energetyczne. W tej sytuacji elektronowa funkcja rozdziału jest równa 1.

W przypadku czynnika związanego ze stanem jąder, czyli g_j, to  jeżeli spiny poszczególnych jąder wynoszą i₁, i_12/, i₃, … to czynnik ten jest dany iloczynem wyrażeń (2i_x + 1), dla każdego jądra, czyli:

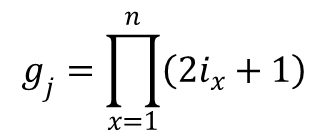
Dla gazu doskonałego złożonego z cząstek jednoatomowych, które mogą mieć tylko energię translacji i elektronową wzór szczegółowy przyjmuje postać:

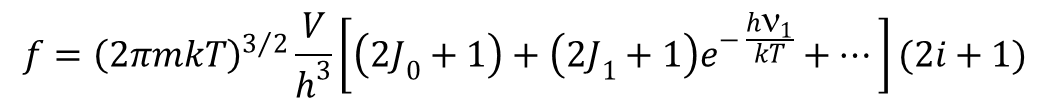
Dla cząstek dwuatomowych mających energie translacji, rotacji i oscylacji i są w stanie podstawowym ¹Σ, mamy:

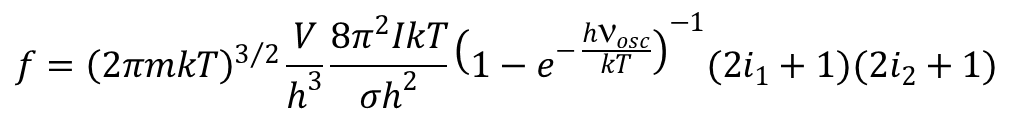
Dla cząstek wieloatomowych o termie podstawowym ¹Σ i wysoko leżących stanach wzbudzonych wzór przyjmuje postać:

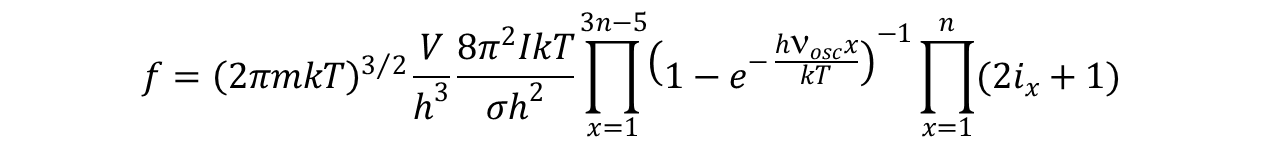
pry czym, gdy w cząsteczce jest n > 3 jąder to różnych oscylacji jest 3n – 5.

Dla nieliniowych cząstek wieloatomowych o termie podstawowym ¹Σ i wysoko leżących stanach wzbudzonych otrzymujemy:

 

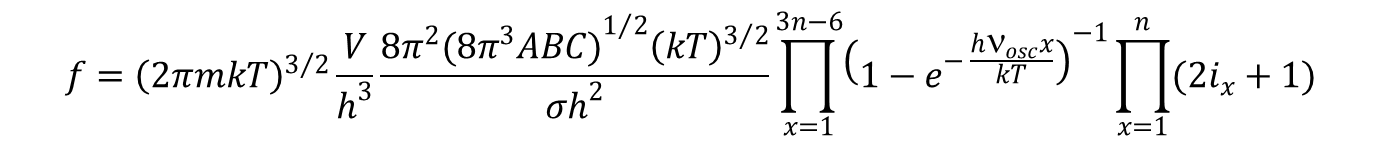
 W tym przypadku liczba różnych oscylacji wynosi 3n – 6.

Entropia, entalpia i ciepło właściwe jako suma funkcji związanych z poszczególnymi funkcjami rozdziału

Jeżeli energię cząstki można przedstawić jako sumę poszczególnych składników to funkcję rozdziału można przedstawić jako iloczyn poszczególnych funkcji. Z tego wynika, że wyrażenie na funkcje termodynamiczne gazu doskonałego  da się przedstawić w postaci sumy członów odnoszących się do poszczególnych funkcji rozdziału.

Entropia mola gazu doskonałego dana jest wyrażeniem:

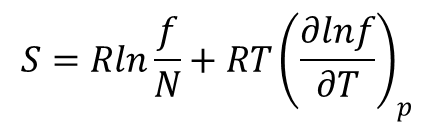
gdy f =f_trf_rotf_oscf_elg_{j od razu widać, że S =} S_tr + S_rot + S_osc + S_e1 + S_j. Gdzie poszczególne składowe są dane wzorami:

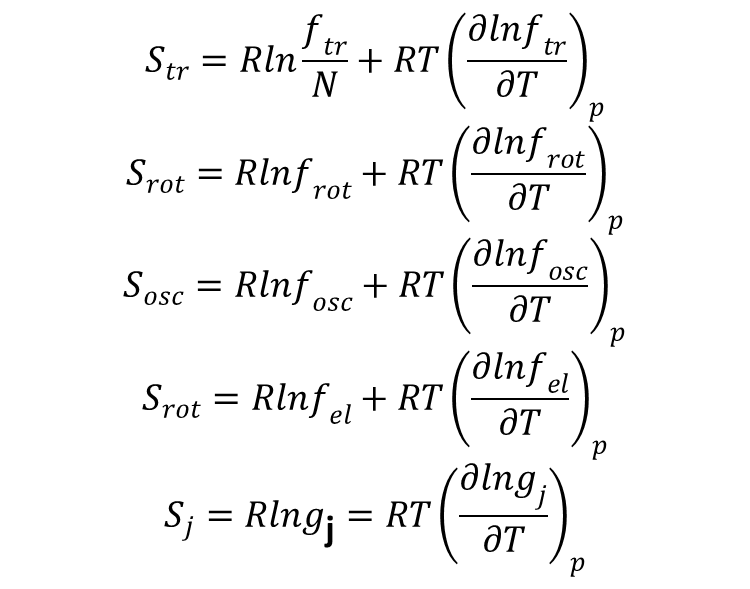
Do przedstawionych powyżej wyrażeń łatwo podstawić odpowiednie wyrażenia na poszczególne funkcje rozdziału.

W taki sam sposób przedstawia się sytuacja z entalpią. Entalpia jednego mola gazu dana jest wzorem:

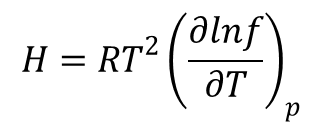
Analogicznie  jak powyżej wyznaczamy odpowiednie składowe entalpii. Dla gazu składającego się z dwuatomowych, homojądrowych cząsteczek o termie podstawowym ¹Σ i wysoko leżących stanach wzbudzonych odpowiednie składowe entalpii są dane następującymi wzorami:

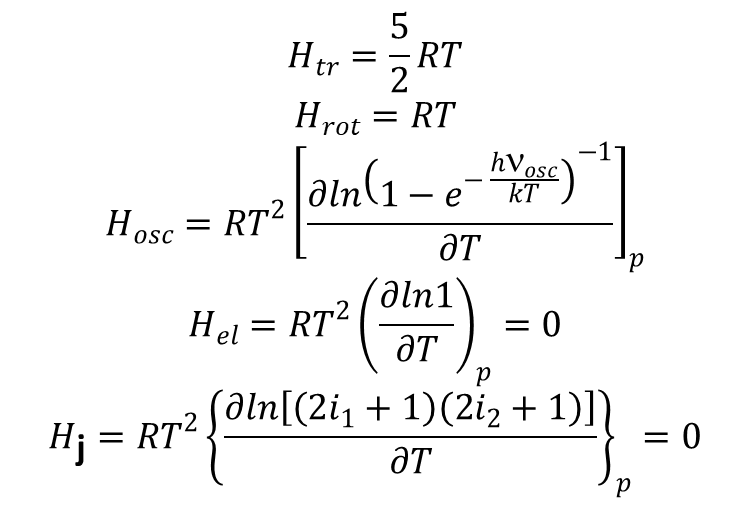
Ostatnie równanie wynika z faktu, że spiny jąder nie zależą od temperatury.

Podobnie znajdujemy wzory na energię wewnętrzną:

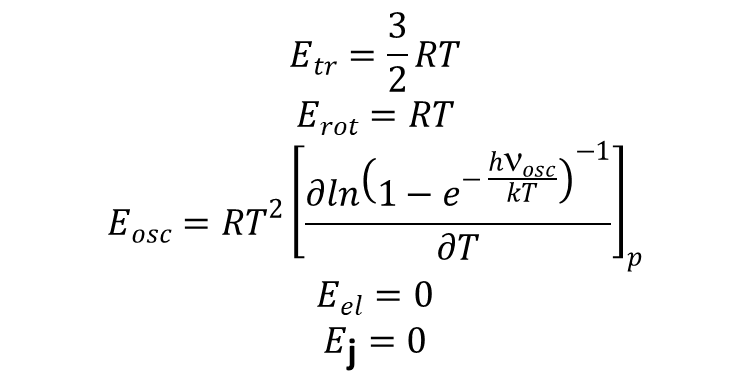
Ciepło właściwe dane wzorem:

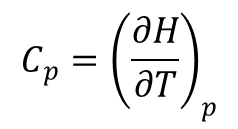
dla gazu doskonałego złożonego z homojądrowych cząsteczek dwuatomowych wyraża się wzorami: