Ruch ciała sztywnego

Ciało sztywne, w mechanice, jest układem punktów materialnych, których odległości się nie zmieniają. Naturalne układy występujące w przyrodzie spełniają ten warunek tylko w przybliżeniu. Realnie istniejące ciała stałe można uważać za ciała ciągłe nie zajmując się ich strukturą wewnętrzną. Przejście od wzorów zawierających sumowanie po punktach nieciągłych do wzorów opisujących ciało ciągłe polega na zamienieniu masy cząstek na masę daną wyrażeniem ρdV, gdzie ρ jest gęstością masy, i całkując po całej objętości ciała dV. Do opisu ruchu ciała sztywnego wprowadzamy dwa układy odniesienia, układ inercjalny (nieruchomy) oraz układ związany z ciałem (ruchomy), Początek układu odniesienia związanego z ciałem jest umieszczony w środku masy ciała. Teraz położenia ciała sztywnego względem nieruchomego układu odniesienia jest całkowicie określone przez podanie położenia ruchomego układu.

Niech R₀ będzie wektorem wodzącym punktu O układu ruchomego. Ponieważ orientacja osi tego układu względem układu nieruchomego jest określona przez trzy niezależne kąty, to położenie ciała sztywnego jest ustalone przez sześć współrzędnych czyli trzy składowe wektora R₀ oraz nntrzy kąty. W ten sposób ciało sztywne jest układem mechanicznym o sześciu stopniach swobody. Teraz rozpatrzmy nieskończenie małe przemieszczenie ciała sztywnego. Możemy je rozłożyć na dwa ruchy. Jednym z niuch jest nieskończenie małe, równoległe przesunięcie ciała, w wyniku którego środek masy przejdzie z położenia początkowego do końcowego przy nie zmienionej osi ruchomego układu odniesienia. Drugi ruch to nieskończenie mały obrót dookoła środka masy, w wyniku którego ciał przechodzi do położenia końcowego. Wektor wodzący dowolnego punktu P ciała sztywnego w ruchomym układzie odniesienia oznaczymy przez r, a wektor wodzący tego samego punktu w układzie inercjalnym przez R. W takim wypadku nieskończenie małe przemieszczenie dR punktu P składa się z przemieszczenia dR₀ wykonanego wraz ze środkiem masy i przemieszczenia [dφr] względem środka masy przy obrocie o nieskończenie mały kąt dφ, czyli:

dR = dR₀ + [dφr]

Dzieląc tę równość przez czas dt i wprowadzając prędkości:

dR/dt = v; dR₀/dt = V; dφ/dt = Ω

otrzymujemy:

v = V + [Ωr]

Wektor V jest prędkością środka masy czyli prędkością postępową. Ω to prędkość kątowa, której kierunek pokrywa się z kierunkiem ruchu osi obrotu. Teraz prędkość v dowolnego punktu ciała względem nieruchomego układu współrzędnych można wyrazić przez prędkość postępowego ruchu ciała i przez prędkość kątową jego obrotu. Do tej pory nie zostały wykorzystane właściwości początku układu współrzędnych jako środka masy ciała. Taki wybór ma znaczenie przy obliczaniu energii poruszającego się ciała. Załóżmy teraz, że początek układu współrzędnych znajduje się nie w środku masy O, lecz w pewnym punkcie O ’ w odległości a od punktu O. Teraz prędkość przemieszczania się środka układu oznaczymy przez V ’, a prędkość kątową obrotu przez Ω ’. I jak poprzednio rozpatrzymy dowolny punkt ciała sztywnego P, którego wektor wodzący względem O ’ oznaczamy przez r’. Zgodnie z powyższym wzorem, do którego podstawiamy r = r’ + a mamy:

v = V + [Ωa] + [Ωr’]

Na podstawie definicji V ’ i Ω ’ wiemy, że v = V ’ + [Ωr’], czyli:

V ’ = V + [Ωa],  Ω ’ = Ω

Z tego jasno widać, że prędkość kątowa z jaką obraca się układ współrzędnych trwale związany z ciałem sztywnym nie zależy od tego układu. Wszystkie takie układy obracają się w danej chwili wokół osi równoległych do siebie z jednakową co do bezwzględnej wartości prędkością Ω. Prędkośc ruchu postępowego nie ma takich właściwości. Prędkości V i Ω są do sienie wzajemni prostopadłe. Z tego wynika, że prędkości v wszystkich punktów ciała leżą w jednej płaszczyźnie, prostopadłej do Ω. Dowolność wyboru układu współrzędnych pozwala tak go umieścić, że V ’ będzie równa zero i ruch ciała sztywnego będzie obrotem wokół osi przechodzącej przez O ’. Oś taka nazywa się chwilową osią obrotu ciała. Jeżeli kierunki V i Ω nie są wzajemnie prostopadłe to wybieramy układ współrzędnych w taki sposób aby stały się równoległe i wtedy ruch w danej chwili składa się z obrotu wokół pewnej osi i ruchu postępowego w kierunku tej osi.

Bezwładność

Przy obliczaniu energii kinetycznej ciała sztywnego traktujemy je jako nieciągły układ punktów materialnych, czyli:

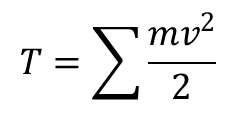gdzie sumowanie obejmuje wszystkie punkty składające się na ciało. Teraz podstawmy za prędkość wartość wyznaczoną wcześniej:

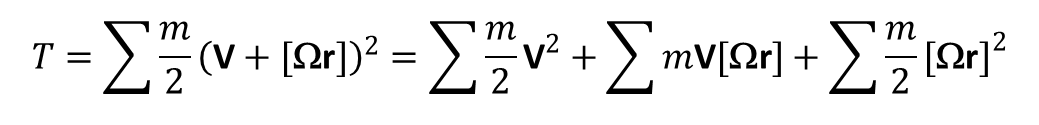Prędkości Vi Ω są równe dla wszystkich punktów ciała sztywnego, w związku z czym przed znak sumy można wyprowadzić V²/2, a  ∑m jest masą ciała, którą oznaczymy przez μ. Drugi wyraz sumy można zapisać w postaci:

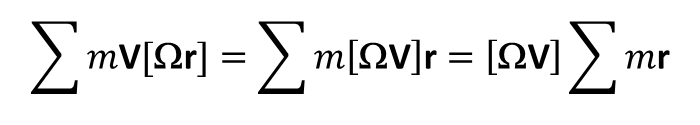i wtedy, jeżeli początek układu odniesienia umieścimy w środku masy będzie on równy 0, gdyż ∑mr = 0. W wyrazie trzecim obliczamy kwadrat iloczynu wektorowego i otrzymujemy:

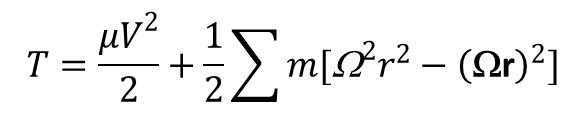W związku z tym energię kinetyczna ciała sztywnego można przedstawić w postaci sumy dwóch wyrażeń. Pierwsze z nich to energia kinetyczna ruchu postępowego wyrażona powyższym wzorem i ma ona taką postać jakby cała masa ciała skupiona była w środku masy. Drugi człon jest związany z energią kinetyczną ruchu obrotowego z prędkością Ω wokół osi przechodzącej przez środek masy. Takie przedstawienie energii kinetycznej ciała sztywnego jest możliwe dzięki wyborowi układu współrzędnych z początkiem w środku masy.

Energię kinetyczną ruchu obrotowego zapiszemy przy pomocy składowych x_i, Ω_i wektorów r i Ω, czyli w postaci tensorowe:

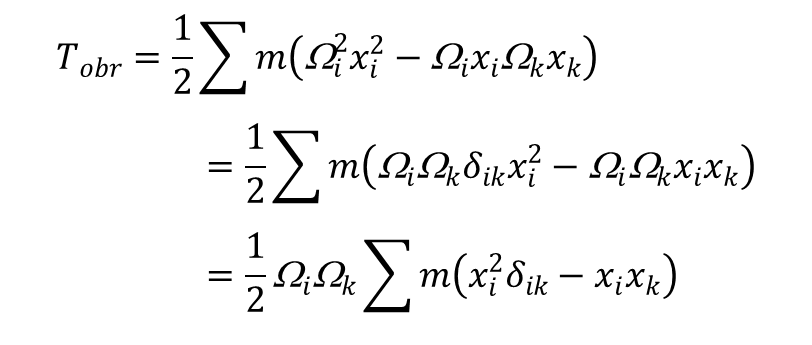δ_ik jest tensorem jednostkowym, a Ω_i = δ_ikΩ_k. Wprowadzając tensor:

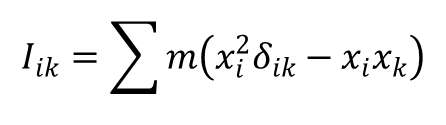wyrażenie na energię kinetyczną ciała sztywnego przyjmuje postać:

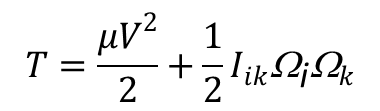Jeżeli od tego wyrażenia odejmiemy energię potencjalną to dostajemy funkcję Lagrange’a. Energia potencjalna jest na ogół funkcją sześciu zmiennych określających położenia ciała czyli x, y, z środka masy i trzech kątów określających orientację osi ruchomego układu współrzędnych względem układu nieruchomego. Tensor I_ik jest tensorem momentu bezwładności i jest symetryczny. Składowe tego tensora w jawnej postaci są następujące:

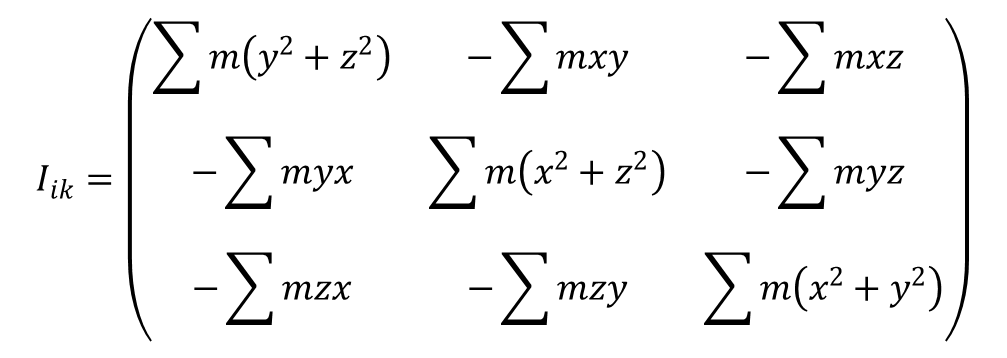Składowe tensora leżące na przekątnej noszą nazwę momentów bezwładności względem odpowiednich osi x, y i z. Jeżeli ciało sztywne traktujemy jako ciągłe to suma w wyrażeniu określającym tensor I_ik przechodzi w całkę po objętości. Tensor bezwładności można sprowadzić do postaci diagonalnej wybierając odpowiednio kierunki x₁, x₂, x₃. Kierunki te noszą nazwę głównych osi tensora bezwładności, a odpowiadające im wartości składowych tensora głównych momentów bezwładności. Każdy z trzech głównych momentów bezwładności nie może być większy od dwóch pozostałych. Ciało, którego trzy główne momentu bezwładności są różne nosi nazwę baka asymetrycznego. Gdy dwa główne kierunki bezwładności są równe mamy do czynienia z bakiem symetrycznym. Gdy trzy momenty bezwładności są równe mamy do czynienia z bąkiem kulistym i wtedy trzy dowolne wzajemnie prostopadłe osie można przyjąć za kierunki główne. Zagadnienie wyboru osi głównych tensora bezwładności upraszcza się gdy ciało sztywne wykazuje jakąś symetrię. W takim wypadku położenie środka masy i kierunki osi głównych też wykazują taką symetrię. Gdy ciało ma płaszczyznę symetrii to środek masy jak i dwie osie główne muszą leżeć w tej płaszczyźnie. Trzecia oś jest do niej prostopadła. Gdy ciało ma oś symetrii dowolnego rzędu to środek masy leży na tej osi i jest ona również jedną z osi głównych tensora bezwładności. Dwie pozostałe osie są do niej prostopadłe. Dalej jeżeli rząd osi symetrii jest większy od 2 to ciało jest bakiem symetrycznym. Wynika to z faktu, że każdą oś główną prostopadłą do osi symetrii można obrócić o kąt 180°. W takim razie wybór osi nie jest jednoznaczny a to ma miejsce tylko w przypadku bąka symetrycznego. Jeżeli układ cząstek tworzących ciało sztywne leży na jednej prostej to dwa główne momenty bezwładności są sobie równe a trzeci jest równy zero. Układ taki nosi nazwę rezonatora. Rezonator ma dwa a nie trzy obrotowe stopnie swobody.

Moment pędu ciała sztywnego

Moment pędu układu mechanicznego zależy od wyboru punktu względem którego się go określa. W przypadku ciała sztywnego najlepiej przyjąć początek układu współrzędnych czyli środek masy ciała za punkt względem którego określany jest moment pędu. W takim przypadku moment pędu ciała jest związany z uchem punktów względem środka masy, czyli:

M = ∑m[r²Ω – r(rΩ)]

Uwzględniając tensor bezwładności można zapisać to równanie w formie:

M_i = I_ikΩ_k

W ogólnym przypadku wektor momentu pędu nie będzie skierowany zgodnie z wektorem Ω. Natomiast w przypadku bąka kulistego wektor momentu pędu jest proporcjonalny do wektora prędkości kątowej i zgodnie z nią skierowany. W przypadku bąka symetrycznego oś obrotu obraca się jednostajnie wokół kierunku wektora momentu pędu opisując stożek kołowy – precesja.

Równania ruchu ciała sztywnego

Ponieważ ciało sztywne ma na ogół sześć stopni swobody to układ równań ruchu powinien składać się z sześciu niezależnych równań. Określić je można przez pochodne czasowe wektorów pędu i momentu pędu ciała. Pierwsze równanie określa siłę działającą na ciało:

Na siłę F składają się tylko siły działające z zewnątrz na ciało, gdyż wszystkie siły wzajemnego oddziaływania cząstek tworzących ciało upraszczają się. Składowymi siły F są pochodne energii potencjalnej ciała względem współrzędnych środka masy. Drugie równanie ruchu określa pochodną czasową momentu pędu M. Wybieramy inercjalny układ odniesienia, w którym w danej chwili środek masy ciała spoczywa i otrzymujemy:

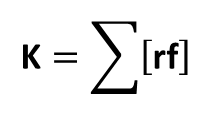Wektor [rf] jest momentem siły f, czyli K jest sumą momentów wszystkich sił działających na ciało.

Funkcja Lagrange’a jednej cząstki w polu zewnętrznym ma postać:

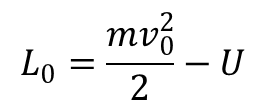a równania ruchu w inercjalnym układzie odniesienia:

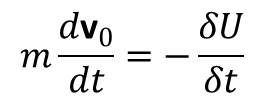Aby przejść do nieinercjalnego układu odniesienia wykorzystujemy zasadę najmniejszego działania. Wtedy równania Lagrange’a:

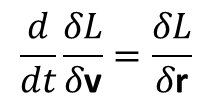zachowują słuszność, ale należy przekształcić funkcję L₀ tak aby je spełniała. Weźmy pod uwagę układ odniesienia K’, który porusza się względem inercjalnego układu odniesienia K ruchem postępowym z prędkością V(t). Prędkości w obydwu układach spełniają związek:

v₀ = v’ + V(t)

Funkcja Lagrange’a w układzie K’ ma postać:

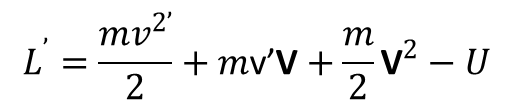Trzeci wyraz w tym równaniu można opuścić ponieważ funkcję V²(t) można przedstawić jako zupełna pochodną względem t inne j funkcji. Ponadto prędkość v’ jest pochodną czasową wektora wodzącego r’ w układzie K’. Definiując przyspieszenie ruchu postępowego układu odniesienia K’ jako W = dV/dt otrzymujemy funkcję Lagrange’a w postaci:

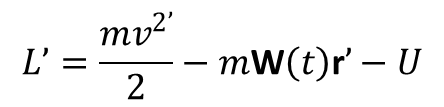Odpowiadającej równania ruchu przyjmują postać:

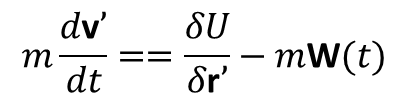Z tego widać, że wpływ przyspieszonego ruchu postępowego układu odniesienia jest równoważny pojawieniu się jednorodnego pola sił, a siła działająca w tym polu jest równa iloczynowi masy cząstki i przyspieszenia W i jest skierowana przeciwnie do tego przyspieszenia.

Gdy układ wykonuje ruch obrotowy z prędkością kątową Ω(t) równanie ruchu przyjmuje postać:

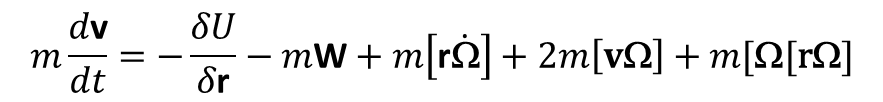Siła 2m[vΩ] jest siłą Coriolisa i zależy od prędkości cząstki, a siła m[Ω[rΩ] to siła odśrodkowa będąca wektorem leżącym w płaszczyźnie przechodzącej przez r i Ω, prostopadłym do osi obrotu i skierowanym od tej osi.