 Principles of Chemistry
Principles of Chemistry
- > Home
-
>
Historia chemii
- > Początki chemii
- > Rozwój alchemii
- > Jatrochemia
- > Badanie spalania i powietrza
- > Odkrycie i badanie gazów
- > Powstanie nowoczesnej chemii
- > Prawa chemiczne
- > Narodziny teorii atomowej
- > Elektrochemia
- > Berzelius, Hisinger, Faraday
- > Początki chemii organicznej
- > Substytucja
- > Wartościowość
- > Chemia fizyczna
- > Rozwój chemii nieorganicznej
- > Struktura atomu
-
>
Pierwiastki
- > Starożytność
- > Średniowiecze
- > Powietrze i woda
- > Analiza chemiczna
- > Halogeny
- > Elektrochemia
- > Metody spektroskopowe
- > Pierwiastki ziem rzadkich
- > Gazy szlachetne
- > Pierwiastki radioaktywne
- > Szeregi pierwiastków promieniotwórczych
- > Pierwiastki otrzymane sztucznie
- > Pierwiastki transuranowe
- > Podsumowanie
- > Układ okresowy
-
>
Mechanika falowa
- > Podstawy teoretyczne
- > Moment pędu
- > Równanie Schrodingera
- > Oscylator liniowy
- > Pole o symetrii sferycznej i pole kulombowskie
- > Spin
- > Identyczność cząstek
- > Oddziaływanie wymienne
- > Druga kwantyzacja
- > Poziomy energetyczne atomów
- > Układ okresowy
- > Atom w polu elektrycznym
- > Atom w polu magnetycznym
- > Cząsteczka dwuatomowa
- > Orto- i parawodór
- > Teoria relatywistyczna
- > Kwantowanie pola elektromagnetycznego
- > Fotony
- > Równanie Diraca
- > Cząstki i antycząstki
- > Atom i cząsteczka
-
>
Związki metali przejściowych
- > Powłoka walencyjna metali przejściowych
- > Efekt Jahna-Tellera
- > Teoria pola krystalicznego
- > Teoria pola ligandów
- > Widma elektronowe
- > Wiązania metal-metal
- > Własności magnetyczne
- > Trwałość związków koordynacyjnych
- > Związki z ligandami π–akceptorowymi
- > Arenowe związki koordynacyjne
- > Oddziaływania agostyczne
- > Wiązania chemiczne
- > Pojęcia chemii nieorganicznej
- > Mechanizmy reakcji
- > Oddziaływania międzycząsteczkowe
- > Elementy fizyki
- > Chemia organiczna
 Symetria
Symetria
Symetria orbitali atomowych i w konsekwencji orbitali cząsteczki związku chemicznego jest jednym z tych elementów, które pozwalają na określenie właściwości jakościowych badanych układów. Przykładem może być określenie liczby i rodzaju poziomów energetycznych atomu czy cząsteczki, które są jednoznacznie determinowane przez symetrię. Rozpatrując jedynie symetrię cząsteczki możemy stwierdzić liczbę stanów energetycznych oraz ilość i rodzaj przejść elektronowych między nimi występujących. Samo rozpatrywanie symetrii pozwala na zdefiniowanie, które z możliwych przejść energetycznych mogą wystąpić, a które nie. Natomiast nie daje możliwości ilościowego wyznaczenia liczbowej różnicy pomiędzy poziomami energetycznymi lub położenia pasm absorpcyjnych. To jest możliwe albo na drodze eksperymentalnej lub obliczeń teoretycznych. Jednak rozpatrywanie symetrii badanego układu stanowi podstawę do zaplanowania eksperymentu i analizy uzyskanych wyników.
Aparatem matematycznym przy rozpatrywaniu symetrii cząsteczek związków chemicznych jest teoria grup, i jako podstawowe narzędzie należy zasygnalizować kilka pojęć koniecznych do zrozumienia dalszego wywodu. Podstawowym pojęciem jest grupa, która stanowi zbiór elementów powiązanych ze sobą pewnymi regułami. To matematyczne pojęcie dla potrzeb rozważań zawężamy do grup utworzonych z operacji symetrii. Jednak pewne podstawowe założenia muszą być spełnione, aby można było zastosować ten aparat matematyczny. Aby utworzyć grupę koniecznym jest spełnienie następujących warunków:
a) iloczyn każdych dwóch elementów grupy łącznie z ich pierwszą potęgą musi być elementem grupy. To stwierdzenie ma szerszy wymiar niż iloczyn algebraiczny i odnosi się do operacji macierzowych;
b) jeden element grupy musi być przemienny (komutować) z wszystkimi innymi elementami i nie zmieniać ich przy mnożeniu. Chodzi tutaj o element jednostkowy oznaczany standardowo jako E;
c) każdy element musi mieć odwrotność, również należącą do grupy.
Grupy mogą być skończone lub nieskończone. Istotnym jest, że każdy wiersz i każda kolumna macierzy zawiera wszystkie elementy grupy, przy czym każdy z nich tylko raz. Ponieważ rozpatrujemy tylko grupy składające się z operacji i elementów symetrii skupmy się na ich zdefiniowaniu i omówieniu. Z matematycznego punktu widzenia operacja symetrii to takie przekształcenie ciała, po którym każdy punkt tego ciała pokrywa się z równoważnym punktem (samym sobą w szczególnym przypadku) przed wykonaniem operacji symetrii. Z punktu widzenia chemika operacja symetrii przeprowadza ciało (cząsteczkę) w położenie równoważne nie różniące się od początkowego, choć niekoniecznie identyczne z nim. Element symetrii jest obiektem geometrycznym, względem którego dokonuje się operacji symetrii. Ponieważ operacje symetrii są związane z elementami symetrii to określa się je względem elementów symetrii, a elementy symetrii wynikają z odpowiednich operacji symetrii. Charakterystyka symetrii cząsteczek wymaga jedynie czterech rodzajów elementów i operacji symetrii. Podane one zostały w tabeli:
| Elementy symetrii | Operacje symetrii |
| Płaszczyzna | Odbicie przez płaszczyznę |
| Środek symetrii | odbicie przez środek symetrii (inwersja) |
| Oś właściwa | Obrót wokół osi |
| Oś niewłaściwa (inwersyjna) | Obrót wokół osi i odbicie przez płaszczyznę prostopadłą do osi obrotu |
Oś symetrii charakteryzuje wielkość zwana krotnością osi, którą definiuje się jako liczbę n równą 360°/α, gdzie α - najmniejszy kąt obrotu wokół rozważanej osi, przeprowadzający układ w położenie nierozróżnialne od poprzedniego. Takie podejście do operacji i elementów symetrii narzuca konieczność traktowania cząsteczek jako zbiorów punktowych atomów, co nie uniemożliwia rozpatrywania poziomów energetycznych cząsteczek.
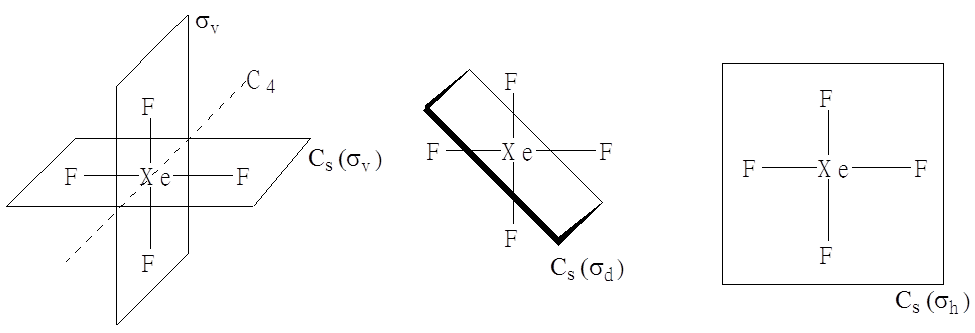 Elementy symetrii dla cząsteczki tetraflurku ksenonuKolejny element symetrii to środek symetrii i związana z nim operacja odbicia w środku symetrii.
Elementy symetrii dla cząsteczki tetraflurku ksenonuKolejny element symetrii to środek symetrii i związana z nim operacja odbicia w środku symetrii.
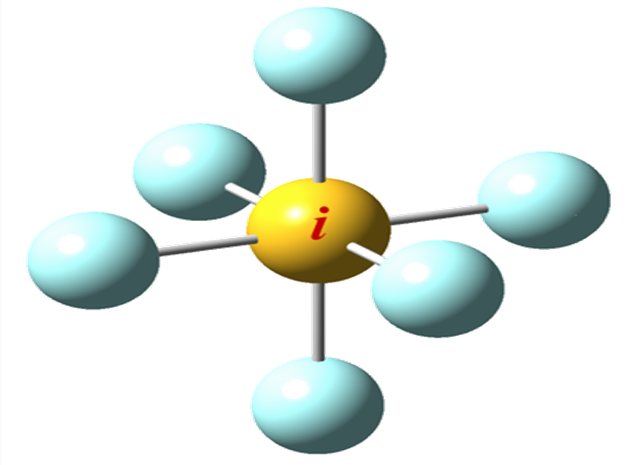 Dalej prześledźmy działanie osi przemiennych, dla których operacją symetrii jest złożenie obrotu o odpowiedni kąt oraz odbicia w płaszczyźnie prostopadłej do tej osi.
Dalej prześledźmy działanie osi przemiennych, dla których operacją symetrii jest złożenie obrotu o odpowiedni kąt oraz odbicia w płaszczyźnie prostopadłej do tej osi.
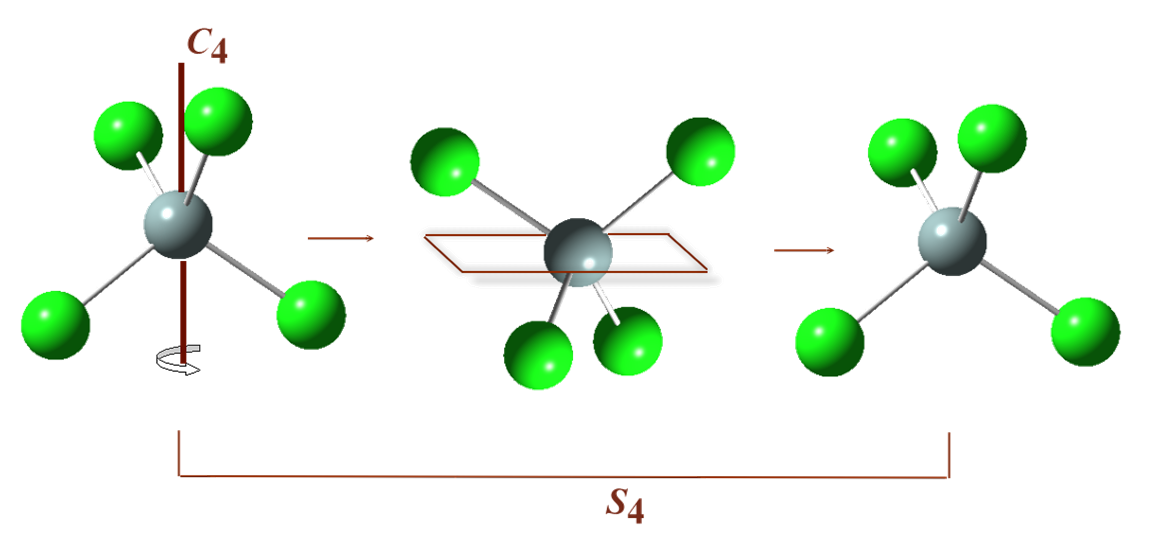 Działanie czterokrotnej osi przemiennejZwróćmy jeszcze uwagę na symetrię występującą w dwóch rodzajach cząsteczek. W dwuatomowych cząsteczkach heterojądrowych mamy do czynienia z osią symetrii o nieskończonej krotności oraz z nieskończoną ilością płaszczyzn symetrii przecinających oś. W dwuatomowych cząsteczkach homojądrowych występuje dodatkowo płaszczyzna symetrii prostopadła do osi oraz środek symetrii.
Działanie czterokrotnej osi przemiennejZwróćmy jeszcze uwagę na symetrię występującą w dwóch rodzajach cząsteczek. W dwuatomowych cząsteczkach heterojądrowych mamy do czynienia z osią symetrii o nieskończonej krotności oraz z nieskończoną ilością płaszczyzn symetrii przecinających oś. W dwuatomowych cząsteczkach homojądrowych występuje dodatkowo płaszczyzna symetrii prostopadła do osi oraz środek symetrii.
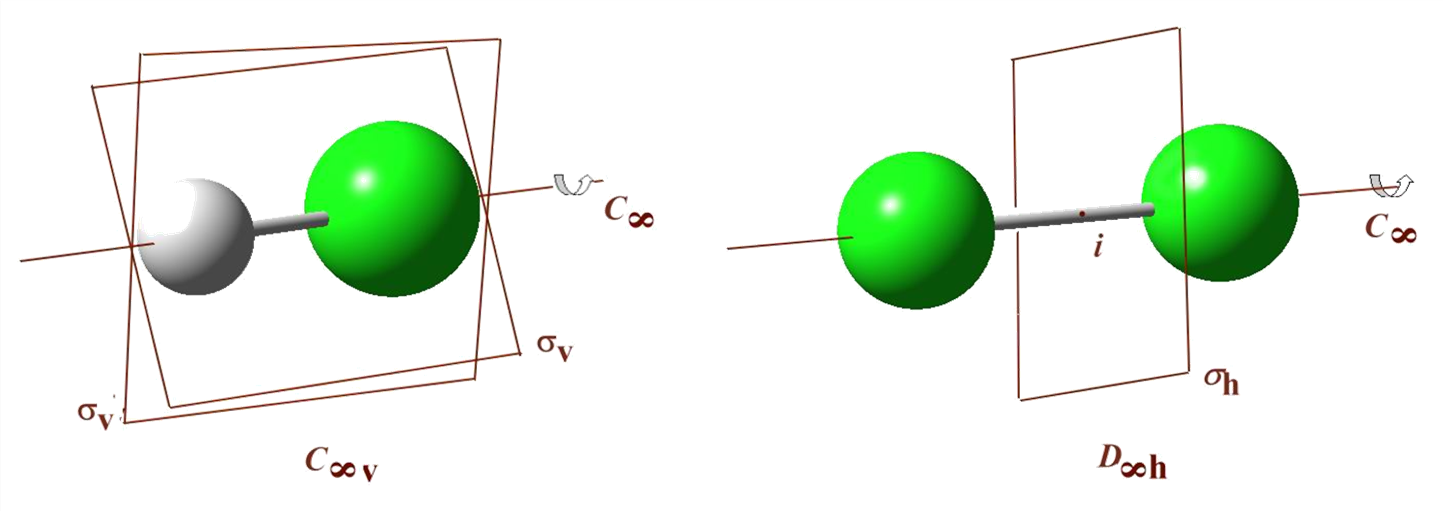 Elementy symetrii w dwuatomowych cząsteczkach hetero– i homojądrowychPrzy opisie symetrii stosuje się dwa rodzaje symboliki. Symbole Schönfliesa składają się z dużych liter C, D, S, T, O określających jeden z pięciu przekształceń symetrii oraz z dolnych indeksów informujących o krotności głównej osi symetrii (n), rodzaju płaszczyzn symetrii (v, h, d) a także istnieniu środka symetrii. Główna oś symetrii ma zawsze kierunek osi z. Symbolika Schönfliesa jest stosowana w dyskusji geometrii i właściwości pojedynczych cząsteczek, a symboliki międzynarodowej (Hermana-Mauguina) używa się przy omawianiu symetrii kryształów.
Elementy symetrii w dwuatomowych cząsteczkach hetero– i homojądrowychPrzy opisie symetrii stosuje się dwa rodzaje symboliki. Symbole Schönfliesa składają się z dużych liter C, D, S, T, O określających jeden z pięciu przekształceń symetrii oraz z dolnych indeksów informujących o krotności głównej osi symetrii (n), rodzaju płaszczyzn symetrii (v, h, d) a także istnieniu środka symetrii. Główna oś symetrii ma zawsze kierunek osi z. Symbolika Schönfliesa jest stosowana w dyskusji geometrii i właściwości pojedynczych cząsteczek, a symboliki międzynarodowej (Hermana-Mauguina) używa się przy omawianiu symetrii kryształów.
Oczywistym jest, że jeżeli jedna operacja symetrii powoduje przejście jakiegoś elementu w inny to zastosowanie tej operacji poprzez działanie operacji odwrotnej wraca do pozycji początkowej, obydwa te elementy są równoważne. Inaczej mówiąc równoważnymi są te elementy (atomy, grupy atomów), które w wyniku działania operacji symetrii mogą się zamieniać ze sobą miejscami. Czyli atomami czy grupami atomów równoważnymi w cząsteczce są atomy (grupy atomów) tego samego rodzaju. Istnienie dwóch elementów symetrii implikuje powstanie przekształcenia symetrii będącego złożeniem przekształceń wynikającym z tych elementów symetrii. Przykładowo: iloczyn dwóch obrotów wokół dwóch osi może być obrotem wokół trzeciej osi. W szczególnym przypadku jeżeli złożymy dwa obroty względem osi x i y o kąt 180o to uzyskujemy obrót względem osi z o ten sam kąt. Iloczyn dwóch odbić w płaszczyznach tworzących dany kąt jest tożsamy z obrotem o podwojoną wartość tego kąta. Istnienie osi o krotności n i płaszczyzny zawierającej tę oś narzuca istnieje n płaszczyzn, z których każde dwie tworzą kąt p/n. Iloczyn dwóch operacji obrotu o kąt 180o wokół osi przecinających się pod danym kątem jest obrotem o podwojoną wartość tego kąta wokół osi prostopadłej do płaszczyzny wyznaczonej przez dwie poprzednie. Oś obrotu wraz z prostopadłą do niej płaszczyzną symetrii generuje środek symetrii. Zależności pomiędzy elementami i przekształceniami symetrii są bardziej złożone niż przedstawia ten krótki wywód, i mogą być opisane w pełni przez rachunek macierzowy. Biorąc pod uwagę powyższe stwierdzenia można podać zawsze ze sobą przemienne (komutujące) operacje symetrii:
1. dwa obroty wokół tej samej osi;
2. odbicia w płaszczyznach prostopadłych do siebie;
3. inwersja wraz z odbiciem lub obrotem;
4. obroty o kąt 180o wokół osi prostopadłych;
5. odbicie w płaszczyźnie i obrót wokół osi obrotu.
Takie podejście pozwala na określenie na przykład warunku do wystąpienia izomerii optycznej. Otóż tylko cząsteczki, które nie dają się nałożyć na siebie w wyniku odbicia zwierciadlanego są izomerami optycznymi. Jak wynika z powyższych rozważań jedynie te cząsteczki, które nie posiadają płaszczyzn ani środka symetrii mogą być optycznie czynne.
Istotnym jest zapoznanie się z punktowymi grupami symetrii stanowiącymi zbiór zupełny operacji symetrii. Odpowiednie rozpatrywanie zależności występujących w symetrii tych grup pozwala na właściwe zrozumienie właściwości badanych układów chemicznych. Istnieje systematyczna procedura określania symetrii cząsteczek pozwalająca na wyciąganie wniosków jakościowych odnośnie ich właściwości spektroskopowych. Sposób postępowania jest następujący:
1. Sprawdzamy czy cząsteczka ma symetrię, w której występują osie nieskończone lub osie wyższego rzędu pozwalające zakwalifikować ją do symetrii heksatetraedru – (Td) lub oktaedru (Oh).
2. Gdy wykluczymy taką symetrię poszukujemy osi symetrii zwykłych i inwersyjnych. W przypadku ich braku szukamy płaszczyzn lub środka symetrii. Jeśli istnieje jedna płaszczyzna symetrii to grupą jest Cs. Jeśli tylko środek symetrii to Ci.
3. Jeżeli występują osie przemienne parzystego rzędu (w praktyce cztero–, sześcio– lub ośmiokrotne) i brak jest osi zwykłych to grupą bazową jest Sn. Istotnym jest parzystość osi inwersyjnych. Jeżeli istnieją inne operacje symetrii to mamy do czynienia z grupami Dn, (klasy z n-krotną osia główną: Dnd – klasa Dn z płaszczyznami odbicia przechodzącymi przez oś najwyższej symetrii i dwusieczne kątów między osiami dwukrotnymi prostopadłymi do tej osi; Dnh – klasa Dn z płaszczyznami prostopadłymi do osi n-krotnej).
4. Gdy nie znaleźliśmy elementów symetrii wymienionych poprzednio szukamy osi najwyższego rzędu. Jeżeli zamiast osi wyższego rządu znajdujemy trzy osie dwukrotne to sprawdzamy czy któraś z nich nie pokrywa się z osią cząsteczki. Jeśli wszystkie osie są tego samego rzędu to za oś główną wybieramy dowolną i odpowiednio wybieramy płaszczyzny poziome i pionowe do niej. Jeżeli wyróżnioną osią jest oś Cn to sprawdzamy czy do niej istnieje n osi dwukrotnych prostopadłych do niej. Jeśli nie to cząsteczka ma symetrię Cn, Cnv lub Cnh.
5. Jeżeli oprócz osi Cn istnieją osie dwukrotne leżące w płaszczyźnie prostopadłej do osi Cn to grupami możliwymi są Dn, Dnh, Dnd. Dn. Gdy brak innych elementów symetrii poza Cn i n osiami dwukrotnymi to grupą symetrii jest Dn. W przypadku obecności dodatkowej płaszczyzny poziomej – grupa Dnh, Dnd występuje gdy płaszczyzny pionowe przechodzą między osiami dwukrotnymi, a płaszczyzny poziomej brak.
Sposób określania grupy punktowej dla danej cząsteczki można przedstawić w postaci schematu czy też algorytmu pozwalającego łatwiej zaklasyfikować cząsteczkę do danej grupy punktowej:

Przenieśmy teraz rozważania czysto intuicyjne na język matematyki. Istotną cechą macierzy kwadratowej jest jej ślad. Ślad macierzy jest sumą jej elementów leżących na głównej przekątnej. Macierze sprzężone mają równe ślady. Istotnym z punktu widzenia naszych rozważań jest przekształcenie punktu (lub zbioru punktów) w przestrzeni. Opierając się na rachunku macierzowym, który w sposób jednoznaczny przedstawia podane wyżej reguły określania symetrii układów chemicznych, wartości x, y, z przekształcają się następująco:
1. tożsamość:
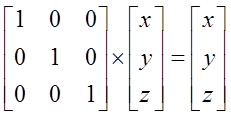
2. odbicie przez płaszczyznę
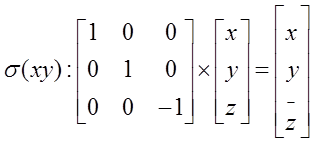
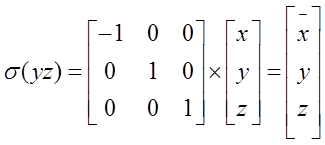
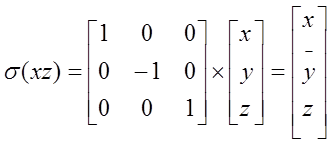
3. inwersja
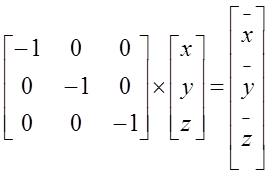
4. obroty wokół osi
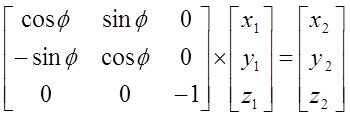
Obroty wokół osi inwersyjnych i przemiennych są nieco bardziej skomplikowane ze względu na złożenie symetrii. Jako przykład przedstawmy działanie osi inwersyjnej.
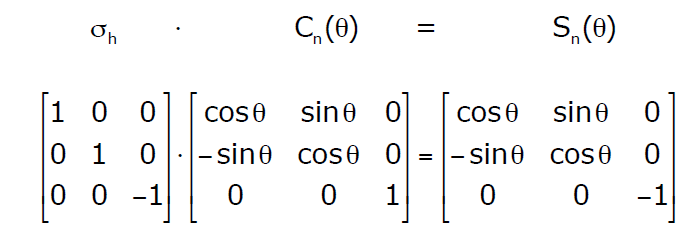
Dla każdej grupy możemy przypisać odpowiednią jej reprezentację czyli jej przedstawienie w postaci macierzowej z uwzględnieniem odpowiednich macierzy operacji symetrii. W ostateczności uzyskujemy macierz, którą możemy zredukować do macierzy o mniejszej liczbie wymiarów. Ostatecznie dochodzimy do postaci, która nie pozwala już na dalszą redukcję postaci blokowej i otrzymujemy reprezentację nieprzywiedlną o najmniejszym możliwym rzędzie. Dla lepszego zrozumienia omówmy konkretne przykłady. Rozpatrzmy cząsteczkę wody, która ze względu na symetrię należy do grupy C2v. Ustawmy cząsteczkę w układzie współrzędnych:
 Z przedstawionego schematu wynika, że odbicie w płaszczyźnie σxz oraz obrót wzdłuż osi z o kąt 180o powinny być sobie równoważne. Jednak zobaczmy jak zmienia się orbital px tlenu przy działaniu tych operacji symetrii.
Z przedstawionego schematu wynika, że odbicie w płaszczyźnie σxz oraz obrót wzdłuż osi z o kąt 180o powinny być sobie równoważne. Jednak zobaczmy jak zmienia się orbital px tlenu przy działaniu tych operacji symetrii.
 Jak widać odbicie w płaszczyźnie xy nie zmienia znaku orbitalu px tlenu, a działanie osi dwukrotnej powoduje taką zmianę. Ten przykład pokazuje jak istotnym narzędziem jest zastosowanie symetrii do opisu cząsteczek. Wracając do elementów symetrii cząsteczki wody stwierdzamy, że mamy do czynienia z czterema operacjami symetrii: E, C2, σv i σ'v. Przyjmując, że płaszczyzny symetrii leżą na osiach xz i yz oraz oś dwukrotna C2 odpowiada osi z układu kartezjańskiego, to macierze opisujące odpowiednie przekształcenia można przedstawić następująco:
Jak widać odbicie w płaszczyźnie xy nie zmienia znaku orbitalu px tlenu, a działanie osi dwukrotnej powoduje taką zmianę. Ten przykład pokazuje jak istotnym narzędziem jest zastosowanie symetrii do opisu cząsteczek. Wracając do elementów symetrii cząsteczki wody stwierdzamy, że mamy do czynienia z czterema operacjami symetrii: E, C2, σv i σ'v. Przyjmując, że płaszczyzny symetrii leżą na osiach xz i yz oraz oś dwukrotna C2 odpowiada osi z układu kartezjańskiego, to macierze opisujące odpowiednie przekształcenia można przedstawić następująco:
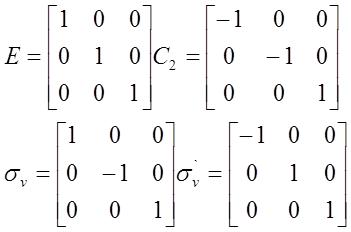 Jeśli dokonamy mnożenia odpowiednich operacji symetrii w tej grupie otrzymamy następującą tabelę:
Jeśli dokonamy mnożenia odpowiednich operacji symetrii w tej grupie otrzymamy następującą tabelę:
|
|
E |
C2 |
σv |
σ'v |
|
E |
E |
C2 |
σv |
σ'v |
|
C2 |
C2 |
E |
σ'v |
σv |
|
σv |
σv |
σ'v |
E |
C2 |
|
σ'v |
σ'v |
σv |
C2 |
E |
Jak widać macierze odpowiednich operacji symetrii podlegają tym samym regułom mnożenia, a każdy element tej grupy jest dla siebie elementem odwrotnym. Zauważmy, że iloczyn obrotu wokół osi C2 i odbicia w płaszczyźnie σv jest tym samym co odbicie w drugiej płaszczyźnie symetrii σv', czyli σv.C2=σv'. Wykonajmy te operacje posługując się macierzami odpowiednich operacji symetrii:
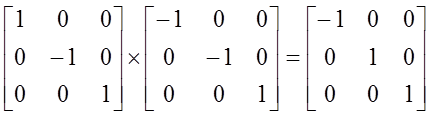 Z kolei każdy element jest sam do siebie elementem odwrotnym. Przykładowo iloczyn dwóch odbić σv. σv=E:
Z kolei każdy element jest sam do siebie elementem odwrotnym. Przykładowo iloczyn dwóch odbić σv. σv=E:
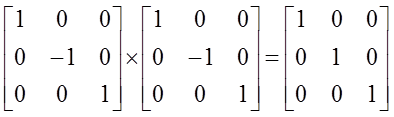 Czyli rozpatrując macierze opisujące operacje symetrii wykonywane na dowolnym punkcie w grupie C2v otrzymaliśmy reprezentację tej grupy. Jednak nie jest to jedyna możliwa reprezentacja rozpatrywanej przez nas grupy. Możemy na osiach x, y i z układu współrzędnych odłożyć trzy wektory i rozpatrywać ich zachowanie podczas działania operacji symetrii tej grupy. Otrzymalibyśmy wtedy macierze 9×9 będące reprezentacją takiej grupy. Jak więc posługiwać się reprezentacjami grup? Biorąc pod uwagę konkretną cząsteczkę związku chemicznego mamy skończoną ilość reprezentacji dowolnego rzędu dla danej symetrii – czyli reprezentację nieprzywiedlną. Znaczenie nie tylko matematyczne mają ślady macierzy grup związane z wielkim twierdzeniem o ortogonalności zgodnie, z którym w zbiorze macierzy tworzących reprezentację nieprzywiedlną zbiór odpowiadających sobie elementów należących do odpowiednich macierzy zachowuje się tak jak składowe jednego wektora w przestrzeni n-wymiarowej, przy czym wektory te są parami ortogonalne i normowane tak, że kwadrat ich długości równy jest stosunkowi wymiaru przestrzeni n do wymiaru reprezentacji czyli rzędu jej macierzy. Z tak ujętego twierdzenia wynika szereg reguł odnoszących się do wymiarów reprezentacji nieprzywiedlnych i ortogonalności wektorów różnych reprezentacji nieprzywiedlnych. Jednak z punktu widzenia chemika eksperymentatora istotnym jest znajomość stosowania teorii grup do badania symetrii cząsteczek. W obecnych czasach nawet wykorzystanie tabeli śladów macierzy poszczególnych grup odbywa się nie na drodze świadomego korzystania, a jedynie poprzez wykorzystanie odpowiedniego oprogramowania komputerowego, w którym zostały one zaimplementowane. Mimo to przedstawmy sposób czytania danych zawartych w tabelach charakterów poszczególnych grup. Powróćmy znowu do grupy C2v, która zawiera cztery elementy, z których każdy tworzy oddzielną klasę. Innymi słowy grupa ta ma cztery reprezentacje nieprzywiedlne, a zgodnie z tym, że suma kwadratów wymiarów nieprzywiedlnych reprezentacji grupy równa jest rzędowi tej grupy musimy znaleźć cztery liczby naturalne spełniające związek: l12 + l22 + l32 + l42 = 4. Oczywistym jest, że rozwiązaniem jest jedynie liczba 1. Czyli grupa C2v ma cztery jednowymiarowe reprezentacje nieprzywiedlne, a tabela śladów macierzy tej grupy ma postać:
Czyli rozpatrując macierze opisujące operacje symetrii wykonywane na dowolnym punkcie w grupie C2v otrzymaliśmy reprezentację tej grupy. Jednak nie jest to jedyna możliwa reprezentacja rozpatrywanej przez nas grupy. Możemy na osiach x, y i z układu współrzędnych odłożyć trzy wektory i rozpatrywać ich zachowanie podczas działania operacji symetrii tej grupy. Otrzymalibyśmy wtedy macierze 9×9 będące reprezentacją takiej grupy. Jak więc posługiwać się reprezentacjami grup? Biorąc pod uwagę konkretną cząsteczkę związku chemicznego mamy skończoną ilość reprezentacji dowolnego rzędu dla danej symetrii – czyli reprezentację nieprzywiedlną. Znaczenie nie tylko matematyczne mają ślady macierzy grup związane z wielkim twierdzeniem o ortogonalności zgodnie, z którym w zbiorze macierzy tworzących reprezentację nieprzywiedlną zbiór odpowiadających sobie elementów należących do odpowiednich macierzy zachowuje się tak jak składowe jednego wektora w przestrzeni n-wymiarowej, przy czym wektory te są parami ortogonalne i normowane tak, że kwadrat ich długości równy jest stosunkowi wymiaru przestrzeni n do wymiaru reprezentacji czyli rzędu jej macierzy. Z tak ujętego twierdzenia wynika szereg reguł odnoszących się do wymiarów reprezentacji nieprzywiedlnych i ortogonalności wektorów różnych reprezentacji nieprzywiedlnych. Jednak z punktu widzenia chemika eksperymentatora istotnym jest znajomość stosowania teorii grup do badania symetrii cząsteczek. W obecnych czasach nawet wykorzystanie tabeli śladów macierzy poszczególnych grup odbywa się nie na drodze świadomego korzystania, a jedynie poprzez wykorzystanie odpowiedniego oprogramowania komputerowego, w którym zostały one zaimplementowane. Mimo to przedstawmy sposób czytania danych zawartych w tabelach charakterów poszczególnych grup. Powróćmy znowu do grupy C2v, która zawiera cztery elementy, z których każdy tworzy oddzielną klasę. Innymi słowy grupa ta ma cztery reprezentacje nieprzywiedlne, a zgodnie z tym, że suma kwadratów wymiarów nieprzywiedlnych reprezentacji grupy równa jest rzędowi tej grupy musimy znaleźć cztery liczby naturalne spełniające związek: l12 + l22 + l32 + l42 = 4. Oczywistym jest, że rozwiązaniem jest jedynie liczba 1. Czyli grupa C2v ma cztery jednowymiarowe reprezentacje nieprzywiedlne, a tabela śladów macierzy tej grupy ma postać:
|
C2v |
E |
C2 |
σv (xz) |
σv' (yz) |
|
|
|
A1 |
1 |
1 |
1 |
1 |
z |
x2, y2, z2 |
|
A2 |
1 |
1 |
–1 |
–1 |
Rz |
xy |
|
B1 |
1 |
–1 |
1 |
–1 |
x, Ry |
xz |
|
B2 |
1 |
–1 |
–1 |
1 |
y, Rz |
yz |
Dla lepszego zrozumienia powyższego wywodu przedstawmy schematycznie działanie poszczególnych reprezentacji na cząsteczkę wody. Jako pierwsze weźmy pod uwagę przesunięcie względem osi y:
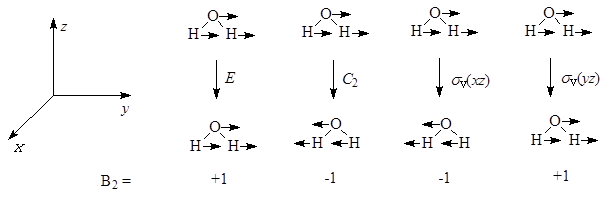 Zbiór składający się z czterech wartości ±1 stanowi nieprzywiedlną reprezentację dla grupy C2v, dodatkowo ta reprezentacja tyczy nie tylko translacji wzdłuż osi y, lecz także wszelkich innych parametrów będących funkcją współrzędnej y, jak orbital py. W związku z tym współrzędna y jest funkcją bazy dla tej nieprzywiedlnej reprezentacji w obrębie grupy C2v, a znak przed cyfrą 1 oznacza symetrię lub antysymetrię zachowania się danego elementu podczas konkretnej operacji symetrii. Jako kolejne weźmy pod uwagę obrót wokół osi C2 i translację wzdłuż osi x i z.
Zbiór składający się z czterech wartości ±1 stanowi nieprzywiedlną reprezentację dla grupy C2v, dodatkowo ta reprezentacja tyczy nie tylko translacji wzdłuż osi y, lecz także wszelkich innych parametrów będących funkcją współrzędnej y, jak orbital py. W związku z tym współrzędna y jest funkcją bazy dla tej nieprzywiedlnej reprezentacji w obrębie grupy C2v, a znak przed cyfrą 1 oznacza symetrię lub antysymetrię zachowania się danego elementu podczas konkretnej operacji symetrii. Jako kolejne weźmy pod uwagę obrót wokół osi C2 i translację wzdłuż osi x i z.

Jak czytać tabele śladów macierzy grup? Zacznijmy od drugiej kolumny, gdzie podane zostały tabele charakterów wszystkich reprezentacji nieprzywiedlnych danej grupy. W kolumnie pierwszej podane są oznaczenia zaproponowane przez Müllikena dla poszczególnych reprezentacji. Wprowadzony system jest następujący:
1. Wszystkie reprezentacje jednowymiarowe oznaczone są literami A lub B, dwuwymiarowe E, a trójwymiarowe symbolem T
2. Te reprezentacje jednowymiarowe, które są symetryczne względem obrotów o kąt 2π/n wokół głównej osi Cn oznacza się jako A natomiast antysymetryczne B
3. Wskaźniki 1 i 2 oznaczają odpowiednio symetrię lub antysymetrię względem osi C2, prostopadłej do osi głównej, lub gdy takiej osi brak do pionowej płaszczyzny symetrii
4. Znaki prim (’) i bis (”) oznaczają symetrię lub antysymetrię względem płaszczyzny σh
5. W przypadku grup zawierających środek symetrii do oznaczeń reprezentacji dopisuje się wskaźniki g (gerade – parzysty) lub u (ungerade – nieparzysty) oznaczające symetrię lub antysymetrię wokół środka symetrii
W trzeciej kolumnie znajduje się sześć symboli x, y, z, Rx, Ry, Rz oznaczających przekształcenia współrzędnych kartezjańskich i obrotów wokół osi. W ostatniej kolumnie podane są kwadraty i iloczyny dwuczynnikowe o odpowiednich własnościach transformacyjnych.
Wartości śladów macierzy dla operacji tożsamej E pozwalają określić maksymalną degenerację orbitali w danej cząsteczce. Dla przedstawionej powyżej tabeli śladów macierzy dla grupy C2v brak jest śladów większych od 1, czyli w cząsteczkach o tej symetrii nie występuje degeneracja orbitali. W przedstawionej w dalszej części tekstu tabeli śladów macierzy dla grupy D3h widać, że istnieje możliwość wystąpienia dwukrotnie zdegenerowanych orbitali.
Kolejnym ułatwieniem, jakie oferuje rozpatrywanie symetrii cząsteczki jest możliwość przewidywania wartości całek nakrywania się orbitali atomowych (Sij=∫φ*φdτ), a tym samym przewidywanie możliwości tworzenia orbitali cząsteczkowych. Ocena całki z iloczynu dwu funkcji przedstawiających w danym przypadku orbitale atomowe opiera się na fakcie, iż wartość każdej całki jest niezależna od orientacji cząsteczki. Innymi słowy całka jest niezależna od każdej operacji symetrii cząsteczki podobnie jak element objętości, po którym wykonywane jest całkowanie. W związku z tym całka ma wartość różną od zera, jeżeli funkcja podcałkowa pozostaje niezmieniona w wyniku działania każdej operacji symetrii grupy punktowej, do której należy rozpatrywana cząsteczka. Jest to zrozumiałe, jeżeli weźmiemy pod uwagę, że zmiana znaku iloczynu dwóch funkcji w wyniku działania operacji symetrii implikuje, że całka z takiego iloczynu jest sumą dwóch udziałów równych, co do wartości ale o przeciwnych znakach czyli równa jest zero. Na gruncie teorii grup możemy stwierdzić, że niezerowy wkład do wartości całek mają te funkcje, dla których ślady macierzy wszystkich operacji symetrii iloczynu funkcji są równe +1. Czyli iloczyn tych funkcji musi mieć typ symetrii A1 lub jemu odpowiadający typ pełnosymetryczny. Te rozważania pozwalają określić, które orbitale atomowe mogą ulegać kombinacji tworząc orbitale cząsteczkowe, a także pozwalają określać reguły wyboru dla przejść elektronowych. Przykładowo w tetraedrze, orbitale s, p oraz dxy, dxz, dyz przekształcają się jak A1 i T2, co wskazuje na udział orbitali typu p w poziomie t2 tetraedru.