Cząsteczka

Próbując rozwiązać równanie falowe dla cząsteczki oprócz przyjęcia przybliżenia nieruchomych jąder musimy poczynić dalsze założenia aby uprościć rachunki. Generalnie wprowadzona dwa różne uproszczenia. Pierwsze z nich wprowadzone przez Heitlera i Londona w roku 1927, które zostało oparte na obliczeniach dotyczących najprostszej cząsteczki H₂. To podejście nosi nazwę teorii wiązań walencyjnych. Drugie podejście do zagadnienia opisu budowy cząsteczek jest związane z rozbudowywaniem powłok elektronowych, gdzie elektronom przypisuje się odpowiednie orbitale. Ta metoda nosi nazwę metody orbitali cząsteczkowych. W teorii wiązań walencyjnych (VB) funkcję falową konstruuje się w sposób podkreślający rolę oddzielnych atomów i zlokalizowanych orbitali atomowych. W metodzie drugiej, orbitali cząsteczkowych, elektronom przypisuje się orbitale obejmujące swoim zasięgiem całą cząsteczkę, co odpowiada ich delokalizacji. Ponieważ z zasady obydwie metody powinny dawać dla tego samego zagadnienia takie same wyniki, to nie powinno mieć znaczenia którą z nich wybierzemy do opisu cząsteczki. Jednak istotna jest prostota obliczeń, a pod tym względem metoda orbitali cząsteczkowych jest znacznie prostsza matematycznie. Metoda wiązań walencyjnych nie jest już praktycznie stosowana, ale pewne koncepcje z niej wynikające są warte uwagi. Jednak to teoria orbitali cząsteczkowych jest ta, która zdominowała opis struktury elektronowej cząsteczek związków chemicznych.

Teoria orbitali cząsteczkowych

Teoria ta powstała z założenia, że główne idee dotyczące budowy elektronowej atomu można zastosować do cząsteczek. W związku z takim podejściem można podać podstawowe zasady na jakich opiera się ta teoria:

1. Każdy elektron w cząsteczce opisywany jest funkcją falową, która reprezentuje go w obrębie całej cząsteczki. Takie ujęcie implikuje, że orbitale cząsteczkowe nie są jednocentrowe a wielocentrowe. Interpretacja modułu kwadratu funkcji falowej opisującej elektron w cząsteczce jest analogiczna do tej jaka została przyjęta dla atomu. Czyli wartość kwadratu funkcji falowej wyraża prawdopodobieństwo znalezienia elektronu w elemencie objętości w pobliżu punktu , w którym wyznaczono wartość funkcji falowej. Możemy również mówić o gęstości chmury ładunku czyli liczbie elektronów przypadających na jednostkę objętości wyrażaną przez kwadrat funkcji falowej.

2. Każdy orbital cząsteczkowy jest charakteryzowany liczbami kwantowymi, które określają jego energię i kształt.

3. Każdemu orbitalowi cząsteczkowemu odpowiada energia, którą można traktować jako energię jonizacji potrzebną do usunięcia elektronu z danego orbitalu. Całkowita energia cząsteczki jest równa sumie energii wszystkich zajętych orbitali z poprawką uwzględniającą wzajemne oddziaływanie elektronów.

4. Każdy elektron w cząsteczce posiada spin które składowa zetowa ma wartość ±½ℏ odpowiadającą spinowej liczbie kwantowej m_s=±½.

5. Zapełniając orbitale elektronami zachowujemy zasadę Pauliego i regułę Hunda.

Istotną cechą orbitali cząsteczkowych jest ich dwucentrowość (wielocentrowość). Gdy elektron znajduje się w pobliżu jednego z jąder to działające na niego siły pochodzą głównie od tego jądra i innych elektronów. Pomijając oddziaływanie pomiędzy elektronami można równanie falowe dla cząsteczki dwuatomowej zapisać w postaci:

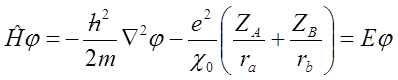gdzie Z_A i Z_B są ładunkami jąder, które można zastąpić efektywnymi ładunkami co w pewnym stopniu pozwala na uwzględnienie oddziaływania pomiędzy elektronami. Jeżeli elektron przebywa w pobliżu jądra atomu A to wpływ na energię układu ma ta część hamiltonianu, która opisuje elektron w polu atomu A. To prowadzi do stwierdzenia, że w pobliżu atomu A orbital cząsteczkowy ma charakter zbliżony do orbitalu atomowego. Analogiczna sytuacja ma miejsce gdy elektron znajduje się w pobliżu atomu B cząsteczki. Ponieważ orbital cząsteczkowy ma charakter orbitali atomów A i B to możemy zapisać orbital cząsteczkowy jako sumę orbitali atomowych:

ψ = c_Aφ_A + c_Bφ_B

Powyższy wzór często przedstawia się w postaci:

ψ = N(φ_A + λφ_B)

N jest stała unormowania, którą często się pomija, a parametr λ jest miarą polarności orbitalu i może przybierać wartości od –∞ do +∞.

Opisane przybliżenie nosi nazwę przybliżenia liniowych kombinacji orbitali atomowych – LCAO (linear combination of atomic orbitals)

Aby orbitale atomowe φ_A i φ_B mogły tworzyć kombinacje muszą zostać spełnione pewne warunki. Otóż energie orbitali atomowych φ_Ai φ_B muszą mieć porównywalne energie i muzą w odpowiednim stopniu nachodzić na siebie. Istotna jest również ich symetria, gdyż φ_Ai φ_B muszą mieć taką samą symetrię względem osi cząsteczki.

Równania wiekowe dla dwuatomowej cząsteczki opisywanej za pomocą przybliżenia LCAO mają następującą postać:

(α_A – E)c_A + (β – ES)c_B=0

(β – ES)c_A + (α_A – E)c_B=0

gdzie α_A = H_AA, α_B = H_BB i β = H_AB. Eliminując z tego układu współczynniki c_A i c_B otrzymujemy równanie:

(α_A – E)(α_B – E) – (β – ES)² = 0

Pierwiastki tego równania E₁ i E₂ określają energię dwóch dozwolonych stanów cząsteczki.

Wielkości α_A, α_B, β i S wyrażają się całkami:

α_A = ∫φ_AĤφ_Adτ;     α_B = ∫φ_BĤφ_Bdτ;     β = ∫φ_AĤφ_Bdτ; S = ∫φ_Aφ_Bdτ.

Teraz widać, że α_A przedstawia w przybliżeniu energię jaką miałby elektron znajdujący się wyłącznie na orbitalu φ_A zlokalizowanym wokół atomu A w cząsteczce. Analogicznie interpretujemy α_B. Całki α_A, α_B noszą nazwę całek kulombowskich ponieważ zawarte w nich są wyrazy odpowiadające oddziaływaniu kulombowskiemu. Generalnie wartości tych całek są większe w przypadku atomów o większej elektroujemności, czyli dla atomów, które silniej przyciągają elektrony. Całki β i S mają duże wartości wtedy gdy nakładanie się orbitali jest duże. Całka S nazywana jest całką nakrywania, a β całką rezonansową. Nazwa całka rezonansowa jest mylące gdyż sugeruje pewien rezonans elektronu pomiędzy obydwoma jądrami w cząsteczce. Nie jest to prawdą, chociaż zapis φ = c_Aφ_A + c_Bφ_B sugeruje, że elektron znajdujący się pomiędzy atomami A i B wykonuje ruch oscylacyjny. Jednak jest to bezpośrednie przełożenie stanu kwantowego na obraz klasycznego ruchu dwóch wahadeł. W rzeczywistości stacjonarny stan kwantowy nie wykonuje żadnych ruchów oscylacyjnych gdyż φ² nie zależy do czasu.

Z przedstawionych powyżej warunków jakie musza zostać spełnione aby kombinacja liniowa orbitali atomowych tworzyła orbital cząsteczkowy wynikają pewne jakościowe zasady. Otóż orbitale walencyjne jednego z atomów nie będą tworzyć kombinacji liniowych z orbitalami wewnętrznych powłok drugiego atomu, co wynika z różnic w energii obydwu orbitali. Kryterium maksymalnego nakładania wskazuje, że silniejsze wiązania powstają w wyniku większego nakładania się orbitali atomów. Natomiast jeżeli S=0 i β=0 wiązanie nie powstaje gdyż rozwiązaniami równań są dwa wyrażenia opisujące stany E=α_A i φ=φ_A oraz E=α_B i φ=φ_B. Takie rozwiązania powstają gdy orbitale użyte do kombinacji nie zachodzą na siebie lub też w przypadku gdy symetria orbitali φ_A i φ_B umożliwia rozdzielenie całek S_AB i β_AB na dwie równe co do wartości bezwzględnej, ale o przeciwnych znakach części. Można to zobrazować na rysunku:

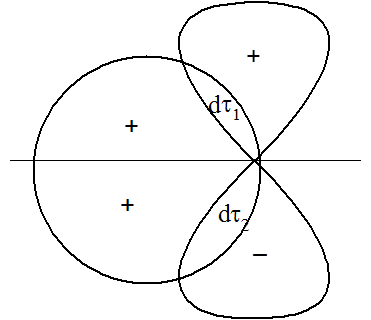 Jak widać, że względu na różnice znaków orbitalu p całka S = ∫φ_Aφ_Bdτ będzie równa zeru, gdyż każdemu elementowi funkcji podcałkowej dτ odpowiada taki sam element równy co do wartości bezwzględnej ale o przeciwnym znaku. Przyjmuje się, że wzdłuż wiązania pomiędzy atomami A i B w cząsteczce znajduje się oś z układu współrzędnych i w związku z tym można określić dozwolone kombinacje orbitali atomowych.

Gdy całka S = ∫φ_Aφ_Bdτ jest równa zeru to funkcje φ_A i φ_B są wzajemnie ortogonalne. Ortogonalne są funkcje będące rozwiązaniami tego samego równania falowego odpowiadające dwóm wartościom energii E_A i E_B.

Najprostszą cząsteczką jest homojądrowa cząsteczka zjonizowanego wodoru H₂⁺. Opis tego układu w metodzie LCAO polega na podaniu funkcji falowej składającej się z orbitali atomowych, czyli:

ψ = c_Aφ_A + c_Bφ_B

Skoro cząsteczka jest homojądrowa to występujące w równaniach wiekowych parametry α_A i α_B muszą być sobie równe, gdyż obydwa centra w cząsteczce są nierozróżnialne i elektron znajdujący się w pobliżu jednego z nich będzie miał taką samą energię jak w pobliżu drugiego. Wyrażenie na energię przyjmuje postać:

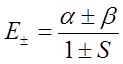
lub równoważnie:

a orbitale cząsteczkowe mają postać φ₊ = N₊(φ_A + φ_B) i φ_– = N_–(φ_A – φ_B). Jeden z orbitali cząsteczkowych leży na skali energii poniżej pierwotnego poziomy a drugi powyżej. Orbital o mniejszej wartości energii nazywamy wiążącym, a wyżej energetyczny antywiążącym. Obrazowo można to przedstawić następująco:

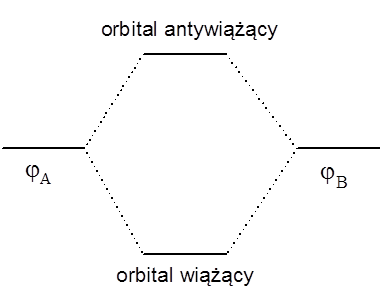Analogicznego diagramu możemy użyć do opisu cząsteczki wodoru H₂. a dwa elektrony 1s atomów wodoru znajdą się na wiążącym orbitali σ cząsteczki.

Powstające w wyniku kombinacji liniowych orbitale cząsteczkowe charakteryzują się odpowiednią symetrią względem osi łączącej jądra atomowe. Orbitale mające nieskończoną oś obrotu wokół osi wiązania oznaczane są symbolem σ. Orbital typu π posiada płaszczyznę węzłową i przy obrocie o połowę kąta pełnego zmienia znak. Natomiast orbital cząsteczkowy powstający w wyniku kombinacji dwóch orbitali d_xy zlokalizowanych na atomach A i B cząsteczki ma dwie płaszczyzny węzłowe i zmienia znak przy obrocie o kąt 90°. Oznacza się go symbolem δ. Kontury wiążących i antywiążących orbitali cząsteczkowych σ i π utworzonych z atomowych orbitali p przedstawione zostały na poniższym rysunku:

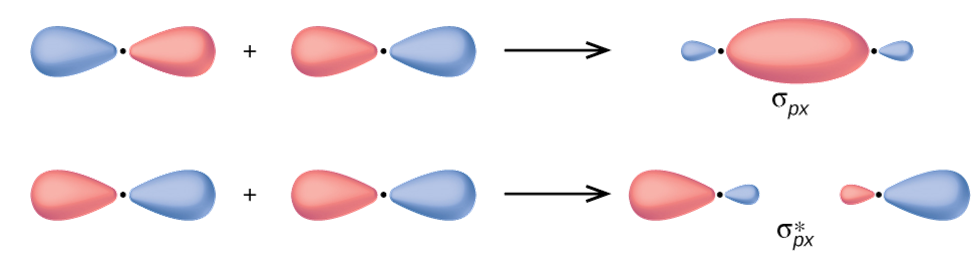
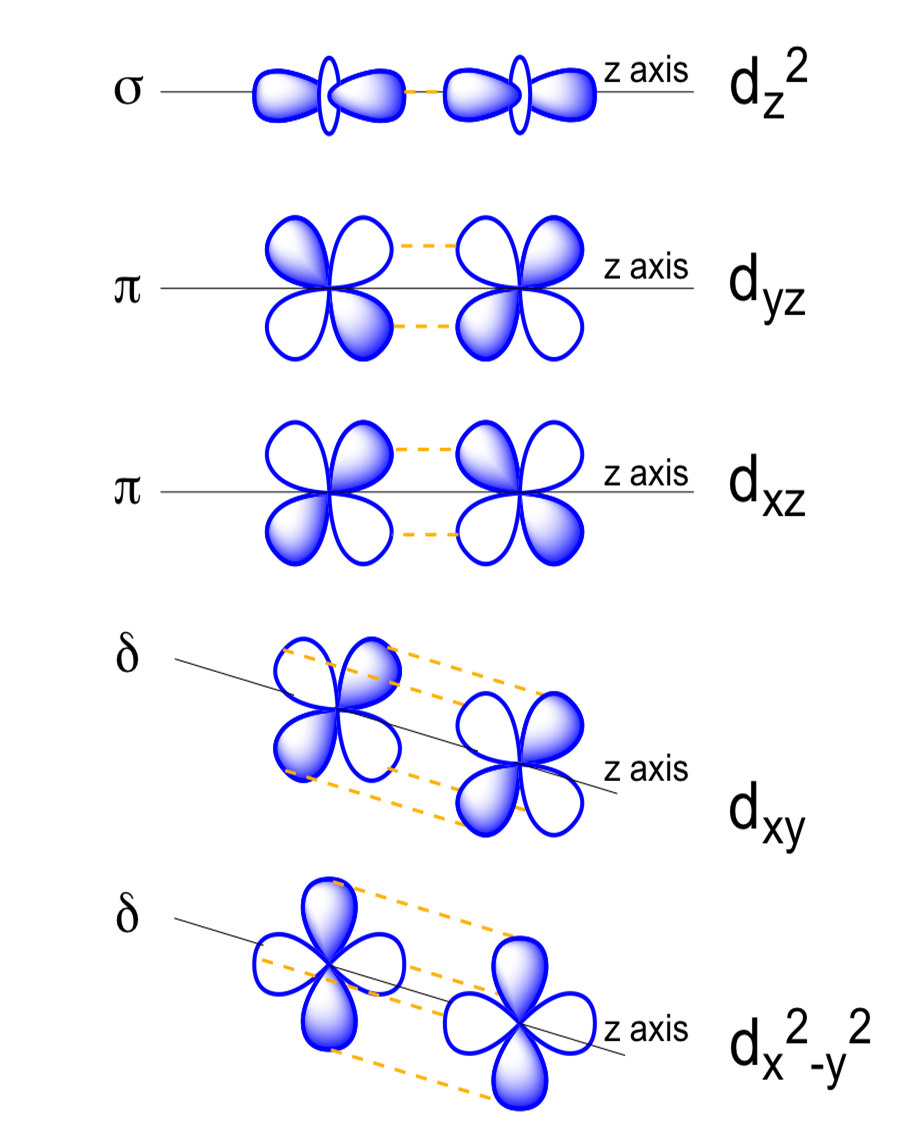
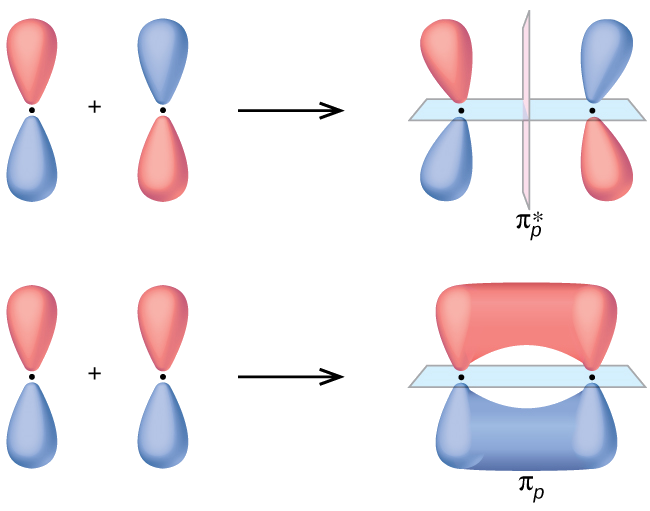Kombinacje orbitali d w zależności od rodzaju orbitalu, dają w wyniku wszystkie typy orbitali cząsteczkowych.

Wygodnym jest posługiwanie się uproszczonymi diagramami korelacyjnymi orbitali cząsteczkowych przy przedstawianiu budowy elektronowej cząsteczek.

Schemat poziomów energetycznych i orbitali cząsteczkowych dla dwuatomowych cząsteczek homojądrowych pierwiastków drugiego okresu, można przedstawić następująco:

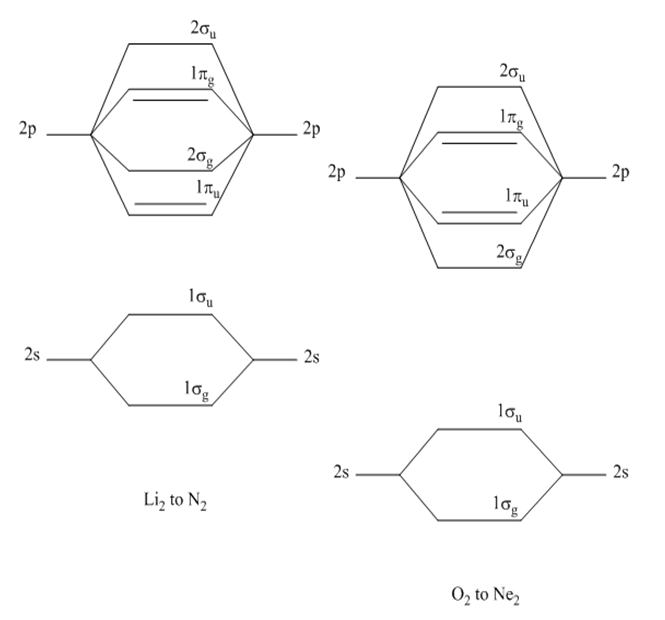W przypadku pierwiastków lżejszych, do azotu, orbitale cząsteczkowe 1π_u są niżej energetyczne niż 2σ_g, dla tlenu i fluoru konfiguracja tych orbitali ulega odwróceniu. Symbole "g" oraz "u" wynikają z symetrii orbitali cząsteczkowych, a ich wyjaśnienie znajduje się w części dotyczącej symetrii.

Heterojądrowe cząsteczki dwuatomowe

W odróżnieniu od dwuatomowych cząsteczek typu A₂, w których wiązanie jest homopolarne, wiązania w cząsteczkach utworzone z dwóch różniących się atomów są spolaryzowane. Przy rozpatrywaniu cząsteczek heterojądrowych przybliżenie LCAO nadal może być stosowane. Reguły jakie muszą spełniać orbitale atomowe brane do liniowej kombinacji pozostają w mocy, a powstające orbitale cząsteczkowe są orbitalami tych samych typów – σ, π, δ –  jak poprzednio.

Weźmy pod uwagę cząsteczkę LiH, w której nie występuje symetria płaszczyzna symetrii pomiędzy jądrami. Orbitalami walencyjnymi atomów w tej cząsteczce są orbital 1s H i 2s litu zawierające każdy po jednym elektronie. Obydwa orbitale mają symetrię typu σ i mogą tworzyć dwa orbitale cząsteczkowe. Ponieważ mamy dwa elektrony, więc zapełniony będzie orbital wiążący i cząsteczka będzie trwała. Diagram poziomów orbitalnych można przedstawić następująco:

Energia orbitalu 1s wodoru jest bliższa co do wartości energii orbitalu wiążącego to możemy przypuszczać, że wiązanie w tej cząsteczce będzie spolaryzowane, a gęstość ładunku na atomie wodoru wzrośnie. Pojęcie gęstości elektronowej (ładunku) na atomie w cząsteczce jest trudne do ścisłego zdefiniowania, gdyż nie sposób określić gdzie kończy się jeden atom a zaczyna drugi w obszarze wiązania. Jednak ze względu poglądowość tego pojęcia jest ono bardzo przydatne. Mülliken zaproponował taką zależność dzięki której można wartość taką określać. Otóż jeżeli orbital cząsteczkowy określa równanie ψ = c_Aφ_A + c_Bφ_B to znormalizowana funkcja falowa ma postać: ψ = 1/N (c_Aφ_A + c_Bφ_B), gdzie N = (c_A² + c_B² + 2c_Ac_BS_AB)^½. W takim przypadku gęstość prawdopodobieństwa znalezienia elektronu wokół atomu A wynosi: 2/N²(c_A² + c_Ac_BS_AB), czyli jest równa gęstości na atomie A plus połowa gęstości wynikającej z nakładania się orbitali. Sposób ten był krytykowany jednak jego prostota oraz możliwość jaką daje przy określaniu typu wiązania chemicznego jest niewątpliwą zaletą. Dodatkowo pojęcie ładunku na atomie samo w sobie jest pojęciem fikcyjnym.

Hamiltonian opisujący cząsteczkę możemy przedstawić w postaci sumy czynników związanych z elektrostatyczną energią potencjalną związaną z jądrem i elektronami rdzenia atomowego, energią kinetyczną, efektami odpychania z pozostałymi elektronami powłoki walencyjnej oraz czynnika związanego z elektrostatyczną energią potencjalną spowodowaną oddziaływaniem z pozostałymi atomami w cząsteczce. W rozważanej cząsteczce LiH orbital 1s litu ma tez symetrię σ i przez to wyrazy H_ij oraz S_ij przyjmują wartości różne od zera. Jednak orbital 1s litu jest zbyt silnie związany aby mógł znacząco oddziaływać z orbitalem 1s wodoru. Natomiast jego wpływ wyrazi się poprzez nieznaczne obniżenie jego energii przy jednoczesnym nieznacznym podwyższeniu energii orbitalu wiążącego σ cząsteczki LiH. Do rozważenia pozostają jeszcze dwa czynniki mające wpływ na trwałość wiązania. Czynnikami tymi są elektrostatyczne przyciąganie elektronów orbitalu o niższej energii uwzględnione w członie H_ii oraz oddziaływanie polegające na kowalencyjnym uwspólnieniu elektronów zawarte w członie H_ij.W cząsteczce wodorku litu wartość H_ii wzrośnie w wyniku odpychania elektronów gdy atom wodoru uzyska ładunek ujemny. Jednocześnie uwzględnienie potencjału elektrostatycznego dodatnio naładowanego atomu litu spowoduje obniżenie wartości H_ii. W związku z tym największy wkład do trwałości cząsteczki LiH w stanie gazowym ma obecność dwóch sparowanych elektronów na orbitalu cząsteczkowym zbliżonym pod względem wartości energii do orbitalu wodoru.

Wyraz H_ij jest związany z mieszaniem się orbitali atomowych, a przez to można go powiązać z kowalencyjnością wiązania. Wielkość wkładu tego czynnika jest zbliżona do różnicy energii |E_i – E_j|, która w przybliżeniu równa jest |H_i – H_j|, pomiędzy orbitalami atomowymi. Przenosząc te rozważania na równanie ψ = c_Aφ_A + c_Bφ_B możemy stwierdzić, że energia orbitalu wiążącego jest znacznie niższa w przypadku gdy φ_A ~ φ_B niż gdy φ_A « φ_B. Jest tp równoznaczne temu, że gdy c_A→1, a c_A→0 to wiązanie w cząsteczce A–B ma bardziej jonowy charakter. Przy dostatecznie dużych wartościach różnicy |E_i – E_j| energia wiązania chemicznego jest zależna jedynie od H_ii i nie zależy od nakładania się orbitali i czynnika H_ij. To stanowi podstawę modelu jonowego wiązania chemicznego. Dodatkowo energia antywiążącego orbitalu zależna jest od czynnika H_ij²/|H_jj – H_ii|, co stanowi podstawę do opisu kierunkowego nakładania się orbitali d metali w cząsteczkach związków koordynacyjnych. W tym przypadku zakłada się, że antywiążący charakter orbitalu jest proporcjonalny do kwadratu całki nakładania tego orbitalu z niskoenergetycznymi orbitalami liganda.

Możemy podsumować powyższe rozważania w następujący sposób:

1. Jeżeli energie orbitali atomowych tworzących wiązanie w cząsteczce są sobie równe to wiązanie pomiędzy nimi ma charakter kowalencyjny, a jego siła wzrasta proporcjonalnie do wartości H_ij czyli nakładania się orbitali atomowych. 

2. Gdy E_A » E_B oraz H_ij ≈ 0 wiązanie będzie miało charakter jonowy, a orbital wiążący w znacznej mierze będzie miał charakter atomowego orbitalu pierwiastka A.

3. Gdy energia E_B jest nieznacznie wyższa od E_A, a |H_ij|>0 to wiązanie będzie miało charakter atomowy spolaryzowany przy większym udziale orbitali atomu A w wiążącym orbitalu cząsteczkowym.

Stan niewiążący wystąpi wtedy gdy:

1. E_B » E_A, a orbital φ_A jest już obsadzony dwoma elektronami. Taka sytuacja występuje w przypadku silnie związanych powłok wewnętrznych. Natomiast gdy E_B ≈ E_A, a φ_A jest zajęty przez dwa elektrony, przykładowo wolna para elektronowa na atomie azotu w NH₃, to wiązanie nadal może zostać utworzone pod warunkiem częściowego przeniesienia ładunku na akceptorowy orbital φ_B. Musi być w tym wypadku spełniony warunek dużego nakładania się orbitali donora i akceptora, czyli wartość H_ij musi być duża.

2. W przypadku gdy E_A ≈ E_B i H_ij ≈ 0, czyli zbliżonych energii orbitali atomów A i B oraz małego nakładania, co nie sprzyja przeniesieniu ładunku powstaje orbital niewiążący.

Można powyższe uogólnienia zastosować do wyjaśnienia kwestii stosunkowo rzadkiego występowania układów rodnikowych, czyli cząsteczek paramagnetycznych. Cząsteczki takie posiadają na powłoce walencyjnej niesparowane elektrony, które są słabo związane z atomem. Dimeryzację dwóch rodników można schematycznie przedstawić następująco:

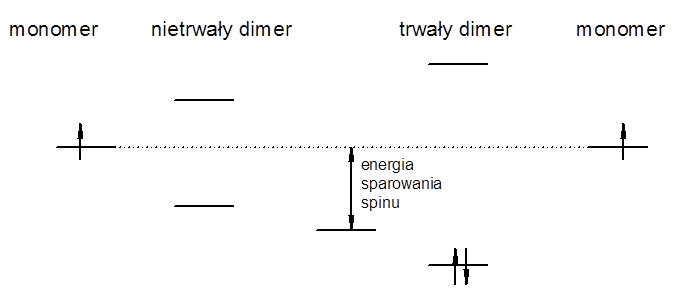Ponieważ rozpatrujemy dwie rodnikowe cząsteczki tego samego związku to energie ich orbitali są takie same. W przypadku gdy energia związana z nakrywaniem się orbitali jest większa niż energia sparowania spinu, korzystna staje się dimeryzacja. Taka sytuacja ma miejsce w szeregu związkach, i w związku z tym układy rodnikowe są spotykane w chemii nieorganicznej stosunkowo rzadko. Natomiast cząsteczki tlenku azotu NO i tlenu O₂ są rodnikami, gdyż w ich przypadku tworzenie dimerów jest niekorzystne ze względu na nikłe nakładanie się orbitali na których zlokalizowane są niesparowane elektrony. Znaczna liczba związków metali przejściowych i pierwiastków ziem rzadkich jest paramagnetyczna, ale nakładanie się dwóch orbitali metali jest praktycznie zerowe, a niesparowane elektrony zajmują orbitale znajdujące się na granicy rdzenia atomowego.