Całkowanie równań ruchu

Ruch jednowymiarowy

Ogólna postać funkcji Lagrange’a dla ruchu układu o jednym stopniu swobody ma postać:

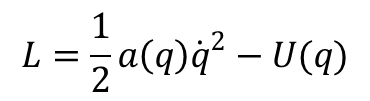gdzie a(q) jest funkcją współrzędnej uogólnionej q, i w przypadku gdy q jest współrzędną kartezjańską to

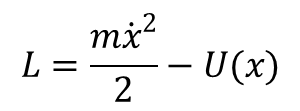Wystarczy przyrównać funkcję L do energii i scałkować równanie różniczkowe pierwszego rzędu:

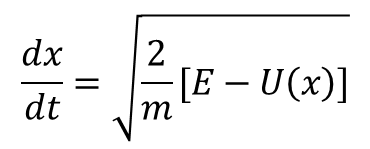uzyskując:

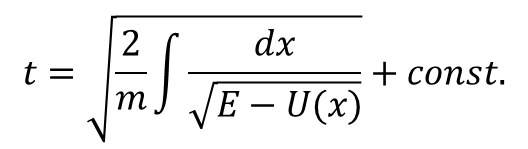Stałymi całkowania są tutaj energia całkowita E i stała całkowania. Energia kinetyczna jest określona dodatnio i w związku z tym podczas ruchu energia całkowita jest zawsze większa od energii potencjalnej, czyli ruch może odbywać się tylko w przedziałach gdzie U (x) < E. Punkty, w których energia potencjalna jest równa energii całkowitej określają granice obszarów, w których ruch może zachodzić. Noszą one nazwę punktów spoczynku, gdyż prędkość w tych punktach jest równa zeru. Ruch jest skończony jeżeli zachodzi w obszarze ograniczonym dwoma punktami spoczynku, w innym przypadku mamy do czynienia z ruchem nieskończonym, kiedy cząstka oddala się nieograniczenie lub przybywa z nieskończoności. Jednowymiarowy ruch skończony jest ruchem drgającym, gdyż cząstka wykonuje okresowo powtarzający się ruch pomiędzy dwoma granicznymi punktami. Zgodnie z odwracalnością czas ruchu pomiędzy punktami x₁ i x₂ jest równy  czasowi ruchu odwrotnego pomiędzy x₂ i x₁. Okres drgań jest równy podwojonemu czasowi potrzebnemu na przebycie odcinka x₁ i x₂ czyli:

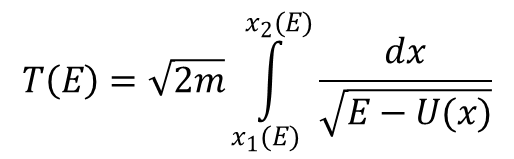Granice całkowania są pierwiastkami równania U (x) = E dla ustalonej wartości E.

Masa zredukowana

Rozpatrzmy układ składający się z dwóch oddziałujących cząstek. Energia potencjalna z jaką oddziałują ze sobą cząstki zależy tylko od odległości pomiędzy nimi, czyli od bezwzględnej różnicy ich wektorów wodzących. Z tego powodu funkcja Lagrange’a ma postać:

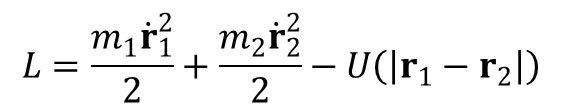 Wprowadźmy wektor względnej odległości punktów:

r = r₁ – r₂

a początek układu współrzędnych umieśćmy w środku masy czyli:

0 = m₁r₁ – m₂r₂

W takim wypadku otrzymujemy:

i równanie na funkcję lagrange’a przyjmuje postać:

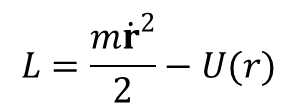Wielkość:

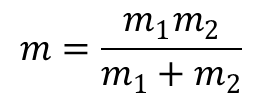nosi nazwę masy zredukowanej, a wprowadzenie jej do równania Lagrange’a powoduje, że funkcja ta staje się formalnie funkcją jednego punktu materialnego poruszającego się w symetrycznym polu zewnętrznym U(r). Zagadnienie ruchu dwóch oddziałujących ciał sprowadza się do rozwiązania zagadnienia ruchu jednego punktu materialnego  w zadanym z góry polu zewnętrznym U)r). Znając rozwiązanie r= r(t) można wyznaczyć tory r₁ = r₁(t) i r₂ = r₂(t), korzystając z powyższych zależności.

Ruch w polu centralnym

Zagadnienie ruchu dwóch ciał sprowadza się do ruchu jednego ciała w polu zewnętrznym, w którym energia potencjalna ciała zależy tylko od jego odległości od określonego, nieruchomego, punktu. Pole takie nosi nazwę pola centralnego , a siła działająca na cząstkę w takim polu skierowana jest w  każdym punkcie równolegle do wektora wodzącego cząstki. Tutaj zachowany jest moment pędu względem środka pola, równy:
M = [rp]

Wektory M i r są wzajemnie prostopadłe, a tym samym stałość M oznacza że przy ruchu cząstki jej wektor wodzący porusza się w płaszczyźnie prostopadłej do M. Innymi słowy ruch cząstki w polu centralnym opisuje krzywa płaska, a funkcję Lagrange’a po wprowadzeniu współrzędnych biegunowych r i φ zapisujemy jako:

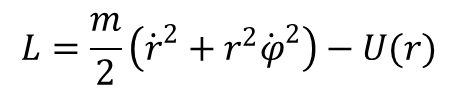Funkcja ta nie zależy od współrzędnej φ, a każdą współrzędną uogólnioną, która nie wchodzi w sposób jawny do funkcji Lagrange’a nazywa się współrzędną cykliczną,. Dla takich współrzędnych mamy:

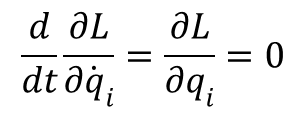W takim wypadku pęd uogólniony:

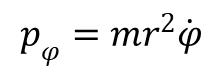jest składową zetową momentu pędu, czyli M_z = M. i jest wartością zachowywaną. Wyrażając φ przez M uzyskujemy wyrażenie na energię w postaci:

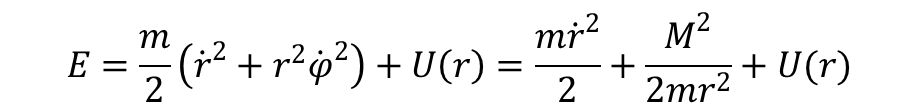 a wyrażenie na φ przybiera postać:

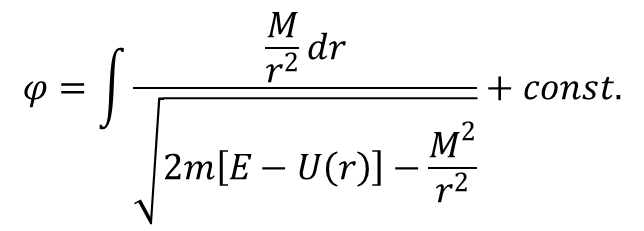Z wyrażenia na energię można wywnioskować, że ruch jednowymiarowy odbywa się w polu o efektywnej energii potencjalnej równej:

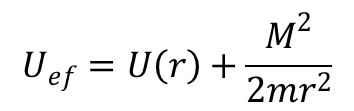w którym wartość dana ułamkiem jest energią odśrodkową. Wartości r, dla których U_ef = E określają granice obszarów, w których ruch może się odbywać.  W tych granicach prędkość radialna jest równa zero, co nie oznacza, że w tych punktach cząstka spoczywa, gdyż prędkość kątowa φ nie musi być równa zeru. Gdy ruch ograniczony jest tylko jedną wartością r ≥ r_min to ruch cząstki jest nieskończony. Gdy obszar zmian r jest zamknięty z dwóch stron tor cząstki leży wewnątrz pierścienia ograniczonego przez okręgi r = r_min i r ≥ r_max. Nie oznacza to, że tor jest krzywą zamkniętą, gdyż wektor wodzący przy zmianie r w granicach od maksimum do minimum zmienia się o kąt równy:

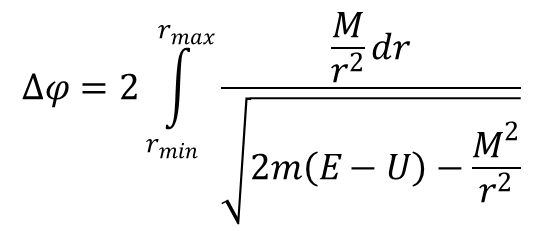Tor taki będzie krzywą zamkniętą wtedy gdy kat ten będzie wymierną częścią kąta 2π. Istnieją dwa typy pól centralnych, w których ruchy skończone mają tory zamknięte i dotyczą one pól, w których energia potencjalna cząstki jest proporcjonalna do 1/r i  do r².

Szczególnym rodzajem pól centralnych są pola, w których energia potencjalna jest odwrotnie proporcjonalna do r, a siła odwrotnie proporcjonalna do r². Przypadek ten obejmuje newtonowskie pole ciążenia oraz kulombowskie pole elektrostatyczne. Na początek rozważmy pole, w którym występują tylko siły przyciągające czyli pole ciążenia. Energia potencjalna takiego pola jest równa U = – α/r, gdzie α jest pewną stałą. 

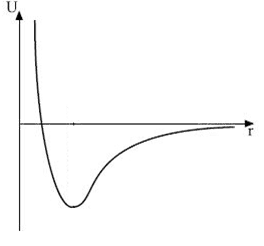Wykres efektywnej energii potencjalnej ma kształt taki jak na rysunku obok. Dla r → 0 energia dąży do nieskończoności, a dla r → ∞ dąży do zera przez wartości ujemne. Minimum funkcja osiąga w punkcie 

r = M²/αm i jest ono równe:

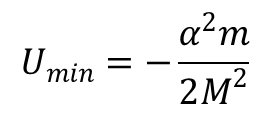Ruch cząstki w takim polu jest nieskończony gdy E ≥ 0, a dla wartości energii mniejszych od zera ruch będzie skończony. Tor ruchu wyraża równanie:

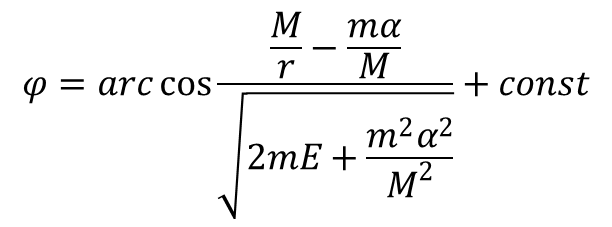 Wybierając kierunek od którego mierzymy kąt φ, w taki sposób aby const = 0 i wprowadzając do wzoru zmienne:

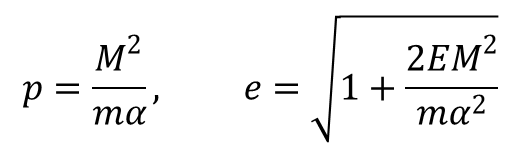 otrzymujemy równanie postaci:

które przedstawia krzywą stożkową o ognisku w początku układu współrzędnych, a p i e są parametrem i mimośrodem tej krzywej. W przypadku gdy rozważamy zagadnienie dwóch ciał to orbita każdego z tych ciał jest również krzywą stożkową, której ognisko znajduje się w środku masy obu ciał. Dla ujemnych wartości energii e < 0 i orbita cząstki jest elipsą, a ruch jest skończony. Dla E > 0 ruch jest nieskończony i jego tor jest hiperbolą. W pobliżu wartości E = 0 cząstka porusza się po paraboli.

W polu sił odpychających (kulombowskie pole elektrostatyczne) U = α/r i w tym przypadku efektywna energia potencjalna maleje monotonicznie od +∞ do 0 przy zmianie r od 0 do ∞. Energia cząstki w takim przypadku może być tylko dodatnia i ruch zawsze jest nieskończony. Torem cząstki jest hiperbola opisana wzorem: