Małe drgania

Najprostszym układem mechanicznym wykonującym ruch w otoczeniu położenia równowagi trwałej jest układ mający tylko jeden stopień swobody. W położeniu równowagi trwałej energia potencjalna U(q) układu ma minimum a wychylenie od tego położenia powoduje powstanie przeciwdziałającej siły dU/dq. Współrzędne uogólnione położenia równowagi oznaczmy przez q₀. Dla małych wychyleń rozwijając różnicę U(q) – U(q₀) w szereg potęgowy względem q – q₀ wystarczy uwzględnić tylko pierwszy nieznikający wyraz, który na ogół jest wyrazem drugiego rzędu:

U(q) – U(q₀) ≈ k/2 (q – q₀)²

 gdzie k = U”(q₀) jest współczynnikiem dodatnim. Cechując energię potencjalną w ten sposób aby w stanie równowagi była równa 0, a wychylenie oznaczając przez x otrzymujemy:

U(x) = kx²/2

W ogólnym przypadku energia kinetyczna układu o jednym stopniu swobody jest równa:

Funkcję a(x) można zastąpić jej wartością w punkcie równowagowym, która będzie równa masie gdy x będzie współrzędną kartezjańską. W takim wypadku funkcją Lagrange’a układu wykonującego jednowymiarowe drgania ma postać:

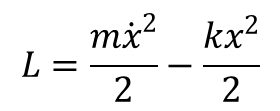Równanie ruchu odpowiadające tej funkcji ma postać:

lub

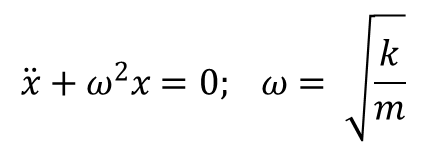Liniowe równanie różniczkowe ma ogólne rozwiązanie postaci:

x = c₁cosωt + c₂sinωt

które można zapisać w postaci

 x = a cos(ωt + α)

Występujące w tych równaniach dowolne stałe a i α wiążą się ze stałymi c₁ i c₂ zależnościami:

Współczynnik a jest amplitudą drgań, a argument funkcji cosinus jest fazą. Wielkość ω jest częstością drgań. Częstość jest podstawową wielkością charakteryzującą drgania niezależną od warunków początkowych, a określoną tylko przez właściwości układu mechanicznego. Takie stwierdzenie jest prawdziwe ale tylko dla małych drgań. matematycznie częstość jest związana z kwadratową zależnością energii potencjalnej od współrzędnej:

E = ½mω²α²

Jak widać energia jest proporcjonalna do kwadratu amplitudy drgań. Często przedstawia się zależność współrzędnej układu drgającego od czasu jako część rzeczywistą wyrażenia zespolonego:

x = Re{Ae^–iωt)

gdzie A jest stałą zespoloną wyrażoną przez A = αe^–iα, co pokazuje, ze jest to amplituda zespolona, której moduł jest równy zwykłej amplitudzie, a argument fazie początkowej.

Drgania wymuszone

Drgania układu, na który działa zewnętrzne zmienne pole noszą nazwę drgań wymuszonych. Ponieważ drgania są małe, to pole zewnętrzne jest na tyle słabe, że nie powoduje zbyt wielkich wychyleń. W takim wypadku obok energii potencjalnej ½kx² występuje również energia U_e(x,t) związana z polem zewnętrznym. W wyrażeniu na energię potencjalną pojawia się wyraz –δU_e/δx opisujący siłę zewnętrzną działającą na układ w położeniu równowagi. Siła ta jest daną funkcją czasu F(x) a do wyrażenia na energię potencjalną dochodzi wyraz – xF(t). W związku z tym funkcja Lagrange’a przyjmuje postać:

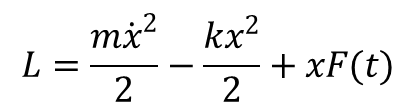Odpowiada jej równanie ruchu postaci:

Rozwiązaniem niejednorodnego równania różniczkowego jest suma wyrażeń opisujących rozwiązanie ogólne równania jednorodnego, w tym przypadku równa rozwiązaniu dla swobodnych drgań układu, oraz całki szczególnej równania niejednorodnego.

Weźmy pod uwagę przypadek gdy siła zewnętrzna jest okresową funkcją czasu o częstości γ:

F(t) = f cos(γt + β)

Szukamy zatem rozwiązania równania ruchu w postaci x = b cos(γt + β). W takim wypadku otrzymujemy b = f/m(ω² – γ²) i dodając ro wyrażenie do rozwiązania równania jednorodnego dostajemy całkę ogólną w postaci:

Stałe a i α określają warunki początkowe. Rozpatrywany układ wykonuje ruch będący złożeniem dwóch drgań odpowiednio z częstością własną ω i z częstością siły wymuszającej γ. Rozwiązanie to nie jest słuszne w przypadku gdy częstość siły wymuszającej jest równa częstości własnej układu. Wtedy mamy do czynienia z rezonansem. W takim wypadku amplituda drgań rośnie liniowo z czasem. aż drgania przestają być małe i powyższe wzory nie znajdują zastosowania. W przypadku drgań w pobliżu rezonansu amplituda zmienia się w sposób okresowy z częstotliwością w określonym przedziale. Zjawisko to nosi nazwę dudnienia. 

Drgania układów o wielu stopniach swobody

Drgania swobodne układów o wielu stopniach swobody opisują podobne zależności jak w przypadku drgań jednowymiarowych. Wyrażenie na energię potencjalną przyjmuje postać:

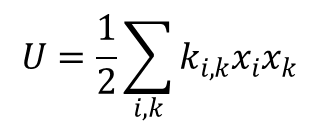Współczynniki k_ik są symetryczne czyli k_ik = k_ki. Podobnie jest w przypadku energii kinetycznej układu, a funkcja Lagrange’a ma postać:

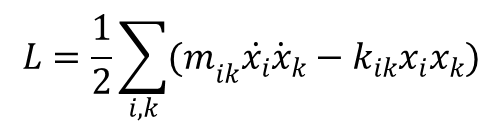Różniczka zupełna funkcji Lagrange’a po uwzględnieniu symetrii współczynników i oraz k ma postać:

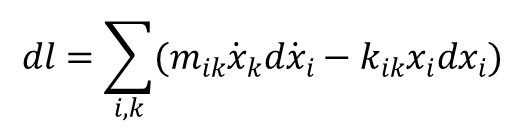a równania Lagrange’a przyjmują postać:

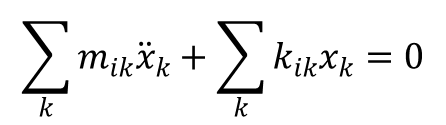Równania te stanowią układ n (i = 1, 2, ..., n) liniowych jednorodnych równań różniczkowych o stałych współczynnikach. Rozwiązując ten układ równań szukamy n niezależnych funkcji x_k(t) postaci:

x_k = A_ke^–iωt

gdzie A_k są pewnymi stałymi. Współczynniki te powinny spełniać układ równań:

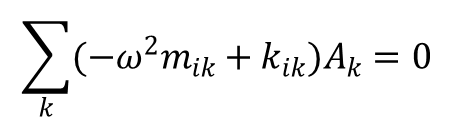Układ powyższych równań algebraicznych będzie miał rozwiązania różne od zera wtedy gdy jego wyznacznik będzie równy zero:

Równania te noszą nazwę równań charakterystycznych i w ogólnym przypadku ich rozwiązaniem jest n różnych, dodatnich pierwiastków, z których każdy określa częstości własne układu. W szczególnych przypadkach niektóre z pierwiastków mogą się pokrywać i wtedy takie częstości noszą nazwę zdegenerowanych. Pierwiastki powyższego równania są rzeczywiste i dodatnie gdyż gdyby ω miało część urojoną to współrzędne i prędkości wzrastałyby wykładniczo z czasem. Występowanie czynnika wykładniczego spowodowałoby zmianę całkowitej energii układu w czasie co jest sprzeczne z zasadą zachowania energii.

Współrzędne uogólnione najlepiej wybrać w taki sposób aby każda z nich reprezentowała jedno drganie harmoniczne. Tak wybrane współrzędne noszą nazwę współrzędnych normalnych, a odpowiadające im drgania harmoniczne są drganiami normalnymi układu. Równania ruchu we współrzędnych normalnych rozpadają się na n niezależnych równań, z których każde z osobna wyznacza jedną niewiadomą. Drgania normalne układu są od siebie zupełnie niezależne. W takim układzie funkcja Lagrange’a we współrzędnych normalnych rozpada się na sumę wyrażeń, z których każde odpowiada jednowymiarowemu drganiu z jedną częstością. W układzie cząstek oddziałujących ze sobą, i nie znajdujących się w polu zewnętrznym, nie wszystkie stopnie swobody mają charakter drgań. Przykładem takich układów są cząsteczki. Obok ruchów reprezentujących drgania atomów wewnątrz cząsteczki wokół położeń równowagi cząsteczka jako całość wykonuje ruch postępowy i obrotowy. Ruchowi postępowemu odpowiadają trzy stopnie swobody, podobnie jak ruchowi obrotowemu. Z tego powodu spośród 3n stopni swobody n-atomowej cząsteczki tylko 3n – 6 stopni swobody odpowiada ruchowi drgającemu. Wyjątkiem są cząsteczki liniowe gdzie mamy tylko 3n – 5 stopni swobody ze względu na to, że ruchowi obrotowemu odpowiadają tylko dwa stopnie swobody (obrót wokół osi cząsteczki nie jest liczony). Drgania normalne cząsteczek klasyfikuje się ze względu na charakter ruchu atomów w cząsteczce, a podstawą tej klasyfikacji jest symetria rozmieszczenia atomów w położeniach równowagi.

Drgania tłumione

 Dotychczas rozpatrywaliśmy ruch odbywający się w próżni. W rzeczywistości podczas ruchu w ośrodku pojawia się opór przeciwdziałający ruchowi. Energia poruszającego się ciała w wyniku oporu ośrodka zamienia się w ciepło, a proces taki nosi nazwę dyssypacji energii. Ruch w tym wypadku nie jest procesem czysto mechanicznym i należy rozpatrywać w takim przypadku ruch ośrodka jak i wewnętrzny stan termodynamiczny i ośrodka jak i ciała. Na ogół przyspieszenie poruszającego się ciała nie jest funkcją tylko jego współrzędnych i prędkości, a tym samym nie istnieją równania ruchu, które można sformułować za pomocą funkcji Lagrange’a. Istnieje jednak pewna kategoria przypadków, kiedy ruch w ośrodku można opisać przy pomocy mechanicznych równań ruchu wprowadzając do nich określone wyrazy dodatkowe. Taki warunek spełniają drgania o częstościach małych w porównaniu z częstościami charakteryzującymi wewnętrzne procesy dyssypacji w ośrodku. W takich wypadkach uważamy, że na ciało działa siła tarcia, która zależy jedynie od jego prędkości. Jeżeli dodatkowo prędkość jest dostatecznie mała to siłę tę można rozwinąć w szereg potęgowy względem prędkości. Wyraz zerowy tego szeregu jest równy zeru bo na ciało w spoczynku siła tarcia nie działa. Pierwszy nie znikający wyraz szeregu jest proporcjonalny do prędkości i w ten sposób uogólnioną siłę tarcia działającą na układ wykonujący małe drgania można zapisać w postaci:

gdzie α jest współczynnikiem dodatnim, x współrzędną uogólnioną, a znak minus oznacza, że siła działa w kierunku przeciwnym do prędkości. Równanie ruchu uwzględniające tę siłę ma postać:

 Dzieląc to równanie przez m wprowadzimy oznaczenia:

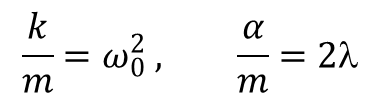Pierwszy iloraz jest częstością drgań swobodnych układu w przypadku niewystępowania tarcia. Wielkość λ nosi nazwę współczynnika tłumienia. Zgodnie z wprowadzonymi symbolami równanie ruchu przyjmuje postać:

 Podstawiając za x = e^rt i rozwiązując równanie otrzymujemy:

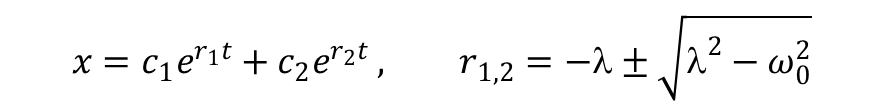Jeżeli λ < ω₀ to otrzymujemy dwie zespolone wartości r sprzężone ze sobą, a rozwiązanie ma postać:

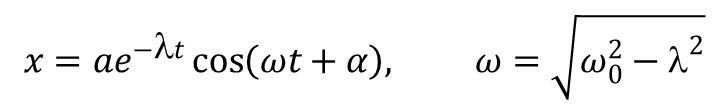a i α są stałymi rzeczywistymi. Wzory te opisują drgania tłumione. Ruch taki można uważać za drgania harmoniczne z amplitudą malejącą wykładniczo. Prędkość malenia amplitudy jest określona przez wykładnik λ. Jeżeli λ małe w porównaniu z ω₀ to w czasie jednego okresu 2π/ω amplituda drgań tłumionych prawie się nie zmienia i można obliczyć wartości średnie kwadratów prędkości i współrzędnej. Ponieważ są one proporcjonalne do e^–2λt to i średnia energia układu maleje zgodnie z równaniem:

E = E₀e^–2λt

gdzie E₀ oznacza energię początkową.

Gdy λ > ω₀ to obie wartości r są rzeczywiste, ruch odbywa się w obecności dużego tarcia i polega na monotonicznym maleniu |x|. Takie tłumienie nosi nazwę tłumienia aperiodycznego. Jeżeli λ = ω₀ ruch nie ma charakteru ruchu drgającego.

Rezonans paramagnetyczny

Rozpatrzmy układy drgające nieodosobnione, w których siła zewnętrzna powoduje zmianę ich parametrów w czasie. Przykładem takiego układu jest wahadło, którego punkt zawieszenia wykonuje ruch okresowy w kierunku pionowym. Równanie ruchu, gdy parametry m i k w funkcji Lagrange’a zależą od czasu, przyjmuje postać:

Wprowadzając zamiast zmiennej t nową zmienną niezależną dτ = dt/m(t) otrzymujemy:

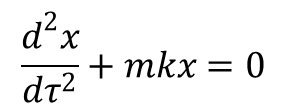 Równanie to można przedstawić w postaci

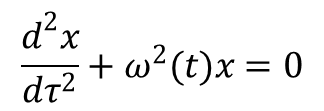ustalając wartość m jako stałą. Postać funkcji ω(t) jest dana przez konkretne warunki początkowe, i możemy założyć że funkcja ta jest okresowa z częstością γ i okresem T = 2π/γ. W takim wypadku ω(t + T) = ω(t), czyli powyższe równanie ruchu jest niezmiennicze względem przekształcenia t → t + T. Jeżeli x(t) jest rozwiązaniem tego równania to funkcja x(t + T) również stanowi jego rozwiązanie. Jeżeli całki x₁(t) i x₂(t) są dwiema niezależnymi całkami tego równania to w wyniku przekształcenia t → t + T przechodzą one w funkcje, które są ich kombinacjami liniowymi. Dalej można obydwa rozwiązania wybrać tak aby ich zmiana  t na t + T sprowadzała się do pomnożenia przez stały czynnik, czyli:

gdzie Π₁(t) i Π₂(t) są okresowymi funkcjami czasu o okresie T. Stałe μ nie mogą być niezależne gdyż funkcje x wiąże równanie:

 Jeżeli funkcje x₁(t) i x₂(t) są dowolnymi funkcjami to zmiana argumentu t na T powoduje pomnożenie przez μ₁μ₂, a powyższe równanie będzie spełnione gdy μ₁μ₂ = 1. Teraz, przyjmując, że powyższe równanie różniczkowe drugiego stopnia ma współczynniki rzeczywiste, to jeżeli x(t) będzie dowolną całką zespoloną tego równania to również funkcja zespolona x*(t) powinna spełniać to równanie. W takim wypadku albo para współczynników μ₁ i μ₂ powinna być identyczna z parą zespolonych, czyli zachodzi równość  μ = μ*, albo współczynniki μ są rzeczywiste, a ich wartości przynajmniej co do modułu muszą być równe 1. W drugim przypadku współczynniki μ równań na x(t) są dodatnia lub ujemną liczbą rzeczywistą różną od 1. Wtedy jedna z funkcji x(t) rośnie wykładniczo z czasem co oznacza, że stan spoczynku układu jest stanem nietrwałym. Oznacza to, że wystarczy układowi nadać dowolnie małe odchylenie od stanu x = 0 aby odchylenie to rosło dowolnie szybko z czasem. Zjawisko to nosi nazwę rezonansu paramagnetycznego. W takim przypadku zmienne położenia i prędkości mające wartości początkowe równe zeru stale będą miały te wartości w przeciwieństwie do zwykłego rezonansu, w którym przesunięcie wzrasta z czasem proporcjonalnie to t również w przypadku zerowych wartości początkowych.

Szczególnym przypadkiem takiego rezonansu jest taki kiedy funkcja ω(t) różni się mało od pewnej stałej wartości i jest funkcją okresową:

gdzie h jest dużo mniejsze od 1 ale jest dodatnie. Najsilniejszy rezonans paramagnetyczny występuje gdy częstość ω(t) jest bliska podwójnej wartości ω₀. Rezonans paramagnetyczny zachodzi w przedziale częstości:

 będącym otoczeniem częstości 2ω₀. Zakresami, w których zachodzi ten rodzaj rezonansu są obszary 2ω₀/n, gdzie n jest liczbą całkowitą, jednak szerokość tych obszarów maleje szybko wraz ze wzrostem n (zgodnie z h²).

Drgania anharmoniczne

W powyższych rozważaniach rozwinięcia energii potencjalnej i kinetycznej na szeregi potęgowe ograniczono do wyrazów drugiego rzędu. Równania ruchu w takim przypadku są równaniami liniowymi a opisywane drgania nazywane są drganiami liniowymi. Przybliżenie to jest prawidłowe dla małych amplitud. Jednak uwzględniając następne człony rozwinięcia uzyskujemy równania opisujące drgania nieliniowe zwane anharmonicznymi. W wyrażeniu na energię potencjalną pojawiają się wyrazy trzeciego stopnia względem współrzędnych, a w energii kinetycznej iloczyny prędkości i współrzędnych nie występujące wcześniej:

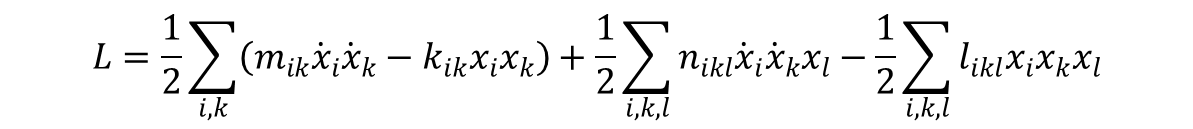gdzie n_ikl i l_ikl są pewnymi stałymi. Rozpatrując wyrazy wyższego rzędu można dojść do wniosku, że pojawiają się drgania o częstościach będących sumami i różnicami drga własnych układu, noszące nazwę drgań kombinacyjnych. Amplitudy tych drgań są proporcjonalne do iloczynów (kwadratów) drgań normalnych. Uwzględniając wyrazy wyższego rzędu uzyskujemy drgania kombinacyjne o częstościach będących sumami i różnicami większej liczby częstości. Już przy rozpatrywaniu trzeciego przybliżenia wśród częstości kombinacyjnych pojawiają się częstości pokrywające się z częstościami wyjściowymi. Wyrazy rezonansowe powodują pojawienie się wyrazów z amplitudą rosnącą w czasie. Z fizycznego punktu widzenia nie jest możliwe aby   amplituda drgań w układzie odosobnionym, nie pobierającym energii z zewnątrz rosła samoczynnie. W rzeczywistości w wyższych przybliżeniach dochodzi do zmiany częstości głównych w porównaniu z "niezaburzonymi" wartościami występującymi w wyrazach kwadratowych na energię potencjalną. Pojawienie się wyrazów wzrastających jest związane z przybliżeniem rozwinięcia w postaci sum funkcji okresowych niesłusznym dla dostatecznie dużych wartości t.