Spin

Pojęcie momentu pędu w mechanice falowej określa właściwości symetrii układu względem obrotów w przestrzeni. Przy obrotach układów współrzędnych 2L+1 funkcji falowych ψ_LM odpowiadających różnym wartościom rzutów momentu pędu M, przekształca się wzajemnie według określonych reguł. W takim wypadku zagadnienie pochodzenia momentu pędu przestaje być istotne, a pojawia się "własny" moment pędu, który należy przypisać cząstce niezależnie od tego czy jest elementarna czy złożona. W ten sposób cząstce przypisuje się w mechanice kwantowej pewien własny moment pędu nie związany z jej ruchem w przestrzeni. Ta właściwość cząstek elementarnych ma specyficznie kwantowy charakter i znika przy przejściu granicznym dla ℏ → 0. Istotną rzeczą jest to, że ta właściwość cząstek nie ma swojego odpowiednika w mechanice klasycznej. Zwłaszcza nie można wyobrażać sobie własnego momentu pędu cząstki jako wyniku jej obrotu wokół własnej osi.

Własny moment pędu nosi nazwę spinu, w odróżnieniu od momentu pędu związanego z ruchem cząstki w przestrzeni, który nosi nazwę orbitalnego momentu pędu. Opis stanu cząstki posiadającej spin musi pozwalać na wyznaczenie prawdopodobieństwa różnych położeń tej cząstki w przestrzeni jak również na wyznaczenie prawdopodobieństwa różnych możliwych orientacji spinu. Innymi słowy funkcja falowa powinna zależeć od trzech zmiennych będących współrzędnymi cząstki i jednej, dyskretnej, zmiennej spinowej wskazującej wartość rzuty spinu na wybraną oś w przestrzeni (zazwyczaj oś z). Zmienną spinową oznaczmy literą σ. W związku z tym funkcja falowa będzie miała postać: ψ(x,y,z,σ) i w rzeczywistości będzie zbiorem kilku różnych funkcji współrzędnych odpowiadających różnym wartościom σ. Całka  ∫|ψ(x,y,z,σ)|²dV określa prawdopodobieństwo tego, że cząstka ma określoną wartość σ. Prawdopodobieństwo tego, że cząstka znajduje się w danym elemencie objętości dV  i jednocześnie ma spin o wartości σ wynosi:

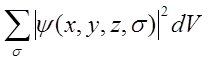Operator kwantowy spinu cząstki przy działaniu na funkcję falową działa tylko na zmienną spinową σ, czyli przekształca on jedne składowe funkcji w drugie. Operatory trzech składowych spinu spełniają te same funkcje komutacyjne co operatory orbitalnego momentu pędu. Jak wiadomo operatory momentu pędu opierają się na ich związku z operatorem nieskończenie małego obrotu i wyrażają ogólne właściwości obrotów jako takich. Ciąg wartości własnych spinu s_z ograniczony jest z dołu i z góry wartościami jednakowymi co do wielkości lecz różniącymi się znakiem, czyli wynosi ±s. Różnica 2s pomiędzy największą i najmniejszą wartością powinna być liczbą całkowitą lub zerem, czyli może przyjmować wartości 0, 1/2, 1, 3/2, ... . Z tego wynika, że:

s² = s(s+1),

gdzie s może być liczbą całkowitą z zerem włącznie, lub liczbą połówkową. Dla danej wartości s rzut spinu może przyjmować wartości: s_z = σ = –s, –s +1, ..., s, a więc 2s+1 wartości. W związku z tym funkcja falowa cząstki posiadającej spin ma 2s+1 składowych. Większość cząstek elementarnych ma spin 1/2, choć istnieją cząstki o spinach równych 0.

Całkowity moment pędu cząstki (J) składa się z jej orbitalnego momentu pędu l i spinu s, a wartości własne całkowitego momentu pędu dane są wzorem:

j = l + s.

Dla danych wartości l i s całkowity moment pędu przyjmuje wartości j = l + s, l + s – 1, ..., |l – s|.

Operator spinu

Zmienna σ różni się od zmiennych określających współrzędne swoją dyskretnością. Ogólna postać operatora liniowego działającego na funkcje zmiennej dyskretnej jest następująca:

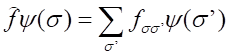gdzie f_αα’ są stałymi.identycznymi z elementami macierzowymi operatora ƒ określonymi za pomocą funkcji własnych operatora ŝ_z.Teraz zamiast całkowania po współrzędnych mamy sumowanie po zmiennej dyskretnej i element macierzowy ma postać:

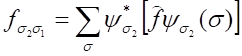gdzie ψ_σ1 i ψ_σ2 są funkcjami własnymi operatora ŝ_z należącymi do wartości własnych s_z = σ₁ i s_z = σ₂.Każda z tych funkcji określa stan, w którym cząstka ma określoną wartość s_z, a tym samym różna od zera jest tylko jedna składowa funkcji falowej:

W takim wypadku operatory działające na funkcje falowe cząsteczki o spinie s można przedstawić w postaci macierzy (2s + 1) –rzędu. W przypadku cząsteczki o spinie połówkowym, czyli s = ½, σ = ½, macierze są rzędu drugiego i mają postać:

ŝ_x = ½σ_x; ŝ_y = ½σ_y; ŝ_z = ½σ_z,

gdzie

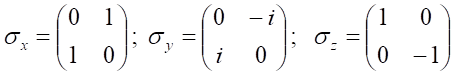Macierze powyższe noszą nazwę macierzy Pauliego. Macierz s_z jest diagonalna jak należało oczekiwać dla macierzy określonej za pomocą funkcji własnej operatora ŝ_z. Wiersze i kolumny w zapisie macierzy Pauliego są numerowane przez wartości σ, przy czym numer wiersza odpowiada pierwszemu, a kolumny drugiemu wskaźnikowi elementu macierzowego. W powyższym przypadku numery te wynoszą ½ i –½. Działanie operatora polega na mnożeniu σ–tego wiersza macierzy przez składowe funkcji falowej zapisane w postaci kolumny:

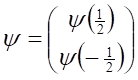
Spinory

Funkcja falowa cząsteczki o spinie zero ma tylko jedną składową, która nie zmienia się podczas obrotów układu współrzędnych, czyli jest skalarem. W przypadku cząsteczki o niezerowym spinie zmianę funkcji falowej przy obrotach wokół osi z powiążemy z operatorem momentu pędu w postaci 1 + iδφ·ŝ_z. Przy obrocie funkcja φ(σ) zmieni się w ψ(σ) + δψ(σ), gdzie δφ(σ) = iδφ­­·ŝ_zψ(σ). Macierz ŝ_z jest diagonalna, a ponieważ jej elementy są równe wartościom s_z = σ to ŝ_zψ(σ) = σφ(σ), czyli δψ(σ) = iσψ(σ)·δφ. To wyrażenie można zapisać w postaci równania różniczkowego dψ/dφ = iσψ, które scałkowaniu pozwala na znalezienie wartości funkcji ψ(σ) po obrocie o dowolny skończony kąt φ. Wartość po obrocie oznaczmy znakiem prim i wynosi ona:

ψ(σ)’ = ψ(σ)e^iσφ

W szczególności przy obrocie o kąt równy 2π wszystkie składowe ψ(σ) zostają przemnożone przez jednakowy czynnik:

e^2πiσ = (–1)^2σ = (–1)^2s

W związku z tym przy pełnym obrocie dookoła osi funkcje falowe cząstek o spinie całkowitym nie zmieniają się, a funkcje falowe cząstek o spinie połówkowym zmieniają znak. Funkcje falowe cząstek o spinie połówkowym mają dwie składowe ψ(½) i ψ(–½). Dla ułatwienia zapisu oznaczmy ψ¹ = ψ^(½) i ψ² = ψ^(–½). Przy dowolnym obrocie układu współrzędnych składowe te podlegają przekształceniu liniowemu:

ψ¹’ = αψ¹ + βψ² , ψ²’ = γψ¹ + δψ²

Współczynniki α, β, γ i δ są zespolone i zależą od kąta obrotu. Aby znaleźć związek między nimi rozpatrzmy układ dwóch elektronów, którego całkowity spin wynosi S = 0 lub S = 1. W pierwszym przypadku układ zachowuje się jak cząstka o spinie 0 i w związku z tym jego funkcja falowa powinna być skalarem. Z drugiej strony jeżeli przyjmiemy, że cząstki tworzące układ nie oddziałują ze sobą to funkcja falowa układu powinna być iloczynem funkcji falowych, z których każda jest funkcją falową jednej cząstki. W takim razie funkcja falowa całości powinna być utworzona ze składowych ψ i φ układu w postaci formy biliniowej:

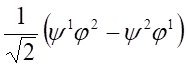antysymetrycznej względem wskaźników 1 i 2. Zastosowanie przekształcenia liniowego do tego układu prowadzi do zależności:

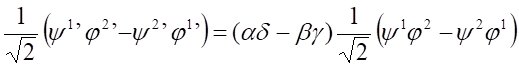wskazującej, ze funkcja układu nie zmienia się przy obrocie układu współrzędnych. Z tego wynika, że jest ona skalarem co prowadzi do zależności pomiędzy współczynnikami α, β, γ i δ wyrażonym zależnością:

αδ – βγ = 1

Skalarem powinno być też wyrażenie

|ψ¹|²  + |ψ²|²  = ψ¹ψ^1*+ ψ²ψ^2*

które określa prawdopodobieństwo znalezienia elektronu w danym punkcie przestrzeni. Porównują to wyrażenie z forma biliniową można zauważyć, że składowe ψ^1* i ψ^2* sprzężone w sposób zespolony z funkcjami falowymi ψ¹ i ψ² powinny przekształcać się przy obrocie jak ψ² i –ψ¹, czyli:

ψ^1*’ = δψ^1* – γψ^2* , ψ^2*’ = –βψ^1* + αψ^2*

Teraz zapisując równania składowych na obrót układu współrzędnych sprzężone w sposób zespolony:

ψ^1*’ = α^*ψ^1* + β^*ψ^2*, ψ^2*’ = γ^*ψ^1* + δ^*ψ^2*

i porównamy je z poprzednimi stwierdzamy, że współczynniki α, β, γ i δ spełniają związki:

α = δ*, β = –γ^*

Z tego jasno widać, że cztery zespolone wielkości α, β, γ, δ zawierają w rzeczywistości tylko trzy rzeczywiste parametry, czyli tyle ile kątów określa obrót w przestrzeni trójwymiarowej.

Wielkość 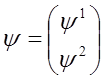mająca dwie składowe i przekształcająca się przy obrotach zgodnie z regułą ψ¹’ = αψ¹ + βψ² , ψ²’ = γψ¹ + δψ² nazywana jest spinorem pierwszego rzędu lub krótko spinorem. Czyli funkcja falowa cząstki o spinie ½ jest spinorem.

Teraz wróćmy do układu zawierającego dwa elektrony i rozpatrzmy stan o spinie S = 1. Funkcja falowa układu powinna mieć trzy składowe odpowiadające rzutom spinu +1, 0, –1. Składowe te są wyrażeniami utworzonymi z iloczynu składowych spinorów ψ i φ, symetrycznych względem swoich wskaźników i przekształcających się przy transformacji zgodnie z powyższą regułą (ψ¹’ = αψ¹ + βψ² , ψ²’ = γψ¹ + δψ²), czyli:

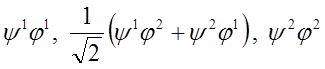Rzut σ całkowitego spinu układu równy jest sumie rzutów spinu obu elektronów. Powyższe funkcje odpowiadają wartościom σ co wynika z sensy wskaźników spinowych 1 i 2 ponieważ oznaczają one rzuty spinów każdego elektronu z osobna. Pierwsza funkcja ma dwa wskaźniki 1, czyli odpowiada rzutowi σ = ½ + ½ = 1, druga ma po jednym wskaźniku 1 i 2 czyli σ = ½ – ½ = 0, a trzecia z dwoma wskaźnikami 2 odpowiada σ = –½ – ½ = –1.

Właściwości spinowe funkcji falowych, będące w istocie własnościami transformacyjnymi funkcji falowych przy obrotach układu współrzędnych są identyczne dla cząstki o spinie 1 i dla układu cząstek o takim spinie całkowitym. Tak samo funkcja falowa cząstki o spinie 2 jest symetrycznym spinorem drugiego rzędu, którego zbiór czterech wielkości ψ¹¹, ψ²², ψ¹², ψ²¹ transformuje się przy obrotach układu współrzędnych jak iloczyny odpowiednich składowych dwu spinorów pierwszego rzędu, ale składowe te nie muszą sprowadzać się do takich iloczynów. Antysymetryczny spinor drugiego rzędu sprowadza się do skalara, gdyż ma tylko jedna niezależna składową (ψ¹¹ = ψ²² = 0, ψ¹² = –ψ²¹). Spinor symetryczny drugiego rzędu ma trzy niezależne składowe gdyż ψ¹² = ψ²¹ odpowiadające składowym funkcji falowej:

Funkcję falową cząstki o spinie 1 można przedstawić w postaci trójwymiarowego wektora Ψ, co wynika z tego że wektor taki jest zbiorem trzech wielkości przekształcających się wzajemnie na siebie. Składowym symetrycznego spinora drugiego rzędu odpowiadają składowe wektora zgodnie z wzorami:

ψ¹¹ = – (ψ_x– i ψ_y),  ψ²² = ψ_x + i ψ_y,  ψ¹² = ψ_z

Te związki oznaczają, że składowe spinora po lewej stronie przekształcają się jak odpowiednie kombinacje składowych wektora po prawej stronie równania. Łatwo to sprawdzić na przykładzie obrotów wokół osi z. Na mocy równości ψ(σ)’ = ψ(σ)e^iσφ i ψ¹ = ψ^(½), ψ² = ψ^(–½) mamy

φ¹’ = e^iiφ/2φ¹ i φ²’ = e^–iiφ/2φ²

gdzie φ¹’ i φ²’  są składowymi spinora w układzie współrzędnych obróconym względem układu początkowego o kąt φ dookoła osi z. Składowe spinora drugiego rzędu wynoszą:

φ¹¹’ = e^iiφφ¹¹, φ¹²’ = φ¹², φ²²’ = e^–iiφφ²²

i takimi samymi wzorami są dane składowe wektora ψ_x – i ψ_y, ψ_x oraz ψ_x + i ψ_y w obu układach współrzędnych. Podobnie można, na podstawie reguł transformacji składowych wektora przy dowolnym obrocie osi współrzędnych, wyprowadzić ogólne reguły transformacji spinorów.

W ogólnym przypadku cząstki o dowolnym spinie funkcja falowa jest spinorem rzędu 2s, symetrycznym względem wszystkich wskaźników. Taki spinor ma 2s + 1 niezależnych składowych. Ponieważ kolejność wskaźników spinora symetrycznego jest nieistotna to tylko te składowe będą różne, które zawierają 2s jedynek i zero dwójek, 2s – 1 jedynek i jedną dwójkę itd. aż do zera jedynek i 2s dwójek. Matematycznie symetryczne spinory n-tego rzędu tworzą nieprzywiedlną reprezentację grupy obrotów. Wymiar tej reprezentacji równy jest 2s + 1 i przyjmuje wartości 1, 2, 3, ... odpowiednio dla s = 0, ½, 1, ... . Reprezentacje utworzone przez funkcje własne orbitalnego momentu pędu ψ_LM są szczególnymi przypadkami, w których wymiary reprezentacji wynoszą 1, 3, 5, ... .