 Principles of Chemistry
Principles of Chemistry
- > Home
-
>
Historia chemii
- > Początki chemii
- > Rozwój alchemii
- > Jatrochemia
- > Badanie spalania i powietrza
- > Odkrycie i badanie gazów
- > Powstanie nowoczesnej chemii
- > Prawa chemiczne
- > Narodziny teorii atomowej
- > Elektrochemia
- > Berzelius, Hisinger, Faraday
- > Początki chemii organicznej
- > Substytucja
- > Wartościowość
- > Chemia fizyczna
- > Rozwój chemii nieorganicznej
- > Struktura atomu
-
>
Pierwiastki
- > Starożytność
- > Średniowiecze
- > Powietrze i woda
- > Analiza chemiczna
- > Halogeny
- > Elektrochemia
- > Metody spektroskopowe
- > Pierwiastki ziem rzadkich
- > Gazy szlachetne
- > Pierwiastki radioaktywne
- > Szeregi pierwiastków promieniotwórczych
- > Pierwiastki otrzymane sztucznie
- > Pierwiastki transuranowe
- > Podsumowanie
- > Układ okresowy
-
>
Mechanika falowa
- > Podstawy teoretyczne
- > Moment pędu
- > Równanie Schrodingera
- > Oscylator liniowy
- > Pole o symetrii sferycznej i pole kulombowskie
- > Spin
- > Identyczność cząstek
- > Oddziaływanie wymienne
- > Druga kwantyzacja
- > Poziomy energetyczne atomów
- > Układ okresowy
- > Atom w polu elektrycznym
- > Atom w polu magnetycznym
- > Cząsteczka dwuatomowa
- > Orto- i parawodór
- > Teoria relatywistyczna
- > Kwantowanie pola elektromagnetycznego
- > Fotony
- > Równanie Diraca
- > Cząstki i antycząstki
- > Atom i cząsteczka
-
>
Związki metali przejściowych
- > Powłoka walencyjna metali przejściowych
- > Efekt Jahna-Tellera
- > Teoria pola krystalicznego
- > Teoria pola ligandów
- > Widma elektronowe
- > Wiązania metal-metal
- > Własności magnetyczne
- > Trwałość związków koordynacyjnych
- > Związki z ligandami π–akceptorowymi
- > Arenowe związki koordynacyjne
- > Oddziaływania agostyczne
- > Wiązania chemiczne
- > Pojęcia chemii nieorganicznej
- > Mechanizmy reakcji
- > Oddziaływania międzycząsteczkowe
- > Elementy fizyki
- > Chemia organiczna
 Cząsteczki wieloatomowe
Cząsteczki wieloatomowe
Cząsteczki typu ML2
Rozpocznijmy omawianie cząsteczek o liczbie atomów większej od dwóch od liniowej cząsteczki fluorku magnezu MgF2. Duża rolę przy rozpatrywaniu struktur elektronowych takich cząsteczek odgrywa symetria, i przypomnijmy, że wiązanie pomiędzy atomami w cząsteczce zgodnie z przyjętym schematem znajduje się na osi z układu współrzędnych. W związku z tym możemy przyjąć, że orbitale 2px i 2py fluoru nie biorą udziału w tworzeniu wiązań z magnezem. Rozwiązując równanie sekularne dla dwóch orbitali 2pz fluoru i orbitalu 3s magnezu otrzymujemy orbitale wiążący, antywiążacy i orbital niewiążący, którego energia przy zaniedbaniu odpychania elektronów będzie równa energii wyjściowych orbitali atomów fluoru. Sytuację można przedstawić dla lepszego zrozumienia następująco. Dwa orbitale φF1 i φF2 przekształcają się jako σu (φF1 – φF2) i σg (φF1 + φF2). Tylko orbital σg będzie oddziaływał z orbitalem 3s magnezu, który też ma symetrię typu σg. Diagram korelacyjny dla tej cząsteczki wygląda następująco:
 Ponieważ energia orbitalu 3pz magnezu jest nieznacznie wyższa od energii orbitalu 3s to należy oczekiwać, że orbital ten będzie nakładał się z orbitalami fluoru, a dodatkowo ze względu na symetrię orbital ten będzie stabilizował niewiążący orbital σu jak to pokazano na powyższym schemacie. To prowadzi do wniosku, że nieobsadzone orbitale atomowe mogą brać udział w wiązaniu gdy różnica energii pomiędzy nimi nie jest zbyt duża oraz gdy ich nakładanie z orbitalami atomów jest dostatecznie duże i posiadają odpowiednią symetrię.
Ponieważ energia orbitalu 3pz magnezu jest nieznacznie wyższa od energii orbitalu 3s to należy oczekiwać, że orbital ten będzie nakładał się z orbitalami fluoru, a dodatkowo ze względu na symetrię orbital ten będzie stabilizował niewiążący orbital σu jak to pokazano na powyższym schemacie. To prowadzi do wniosku, że nieobsadzone orbitale atomowe mogą brać udział w wiązaniu gdy różnica energii pomiędzy nimi nie jest zbyt duża oraz gdy ich nakładanie z orbitalami atomów jest dostatecznie duże i posiadają odpowiednią symetrię.
Cząsteczka fluorku magnezu jest liniowa, natomiast dla nieliniowych cząsteczek typu ML2 symetria ulega obniżeniu z C∞v do C2v. z dwukrotną osią symetrii wzdłuż osi z. Zgodnie z symetrią takiego układu odpowiednie orbitale transformują się jako a1, b1 i b2, tak jak pokazano to na poniższym schemacie.
 Natomiast diagram orbitali cząsteczkowych jest następujący:
Natomiast diagram orbitali cząsteczkowych jest następujący:
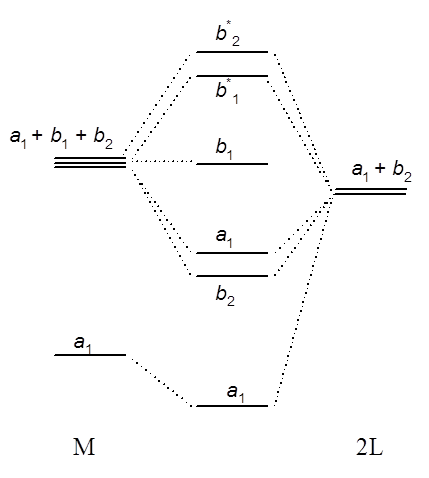 Orbital b2 typu σ ligandu może nakładać się z orbitalem py, natomiast a1 typu σ może nakładać się z orbitalem pz oraz s atomu M. O tym, który z orbitali s czy pz będzie miał większy udział w wiązaniu decydują wartości energii. Zastanówmy się co stanie się z poziomami energetycznymi cząsteczki gdy kąt L–M–L będzie się zwiększał aż do kąta 180° czyli do momentu gdy cząsteczka stanie się liniowa. Biorąc pod uwagę zmianę symetrii cząsteczki stwierdzamy, że orbital b2 w cząsteczce liniowej staje się orbitalem σu, dwa pozostałe orbitale p atomu M stają się orbitalami niewiążącymi typu πu. Orbital a1 wywodzący się z orbitali typu s odpowiada wiążącemu orbitalowi cząsteczkowemu σg.
Orbital b2 typu σ ligandu może nakładać się z orbitalem py, natomiast a1 typu σ może nakładać się z orbitalem pz oraz s atomu M. O tym, który z orbitali s czy pz będzie miał większy udział w wiązaniu decydują wartości energii. Zastanówmy się co stanie się z poziomami energetycznymi cząsteczki gdy kąt L–M–L będzie się zwiększał aż do kąta 180° czyli do momentu gdy cząsteczka stanie się liniowa. Biorąc pod uwagę zmianę symetrii cząsteczki stwierdzamy, że orbital b2 w cząsteczce liniowej staje się orbitalem σu, dwa pozostałe orbitale p atomu M stają się orbitalami niewiążącymi typu πu. Orbital a1 wywodzący się z orbitali typu s odpowiada wiążącemu orbitalowi cząsteczkowemu σg.
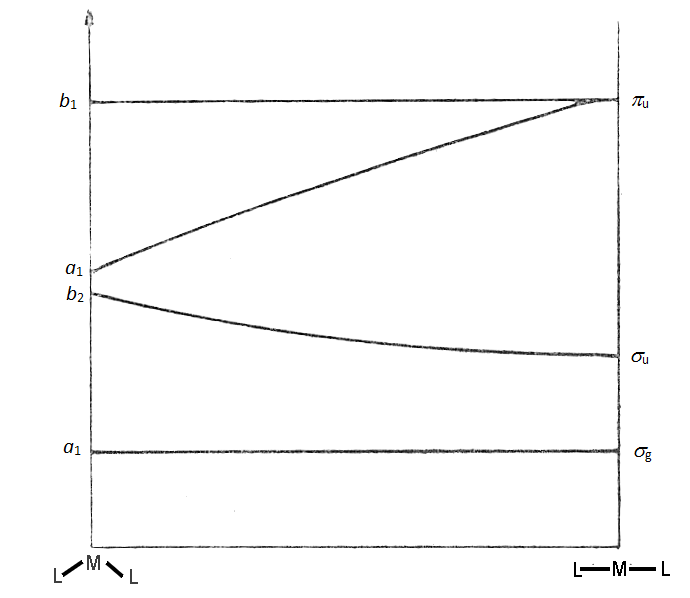 Diagram Walsha obrazujący korelację orbitali cząsteczkowych dla zgiętej i liniowej cząsteczki trójatomowej.Opierając się na diagramie Walsha możemy stwierdzić, że orbital px jest zawsze niewiążący (wiązania w cząsteczce są ułożone wzdłuż osi y), a jego energia zmienia się nieznacznie przy zmianie geometrii cząsteczki z liniowej do zgiętej. Orbital pz w cząsteczce liniowej przekształca się z wiążącego w niewiążący, a jego energia wzrasta. Energia orbitalu b2 (py) zmniejsza się w cząsteczce liniowej gdyż nakładanie z orbitalami atomów L jest większe. Zmiany energii orbitalu a1 (s) są nieznaczne przy zmianie geometrii cząsteczki.
Diagram Walsha obrazujący korelację orbitali cząsteczkowych dla zgiętej i liniowej cząsteczki trójatomowej.Opierając się na diagramie Walsha możemy stwierdzić, że orbital px jest zawsze niewiążący (wiązania w cząsteczce są ułożone wzdłuż osi y), a jego energia zmienia się nieznacznie przy zmianie geometrii cząsteczki z liniowej do zgiętej. Orbital pz w cząsteczce liniowej przekształca się z wiążącego w niewiążący, a jego energia wzrasta. Energia orbitalu b2 (py) zmniejsza się w cząsteczce liniowej gdyż nakładanie z orbitalami atomów L jest większe. Zmiany energii orbitalu a1 (s) są nieznaczne przy zmianie geometrii cząsteczki.
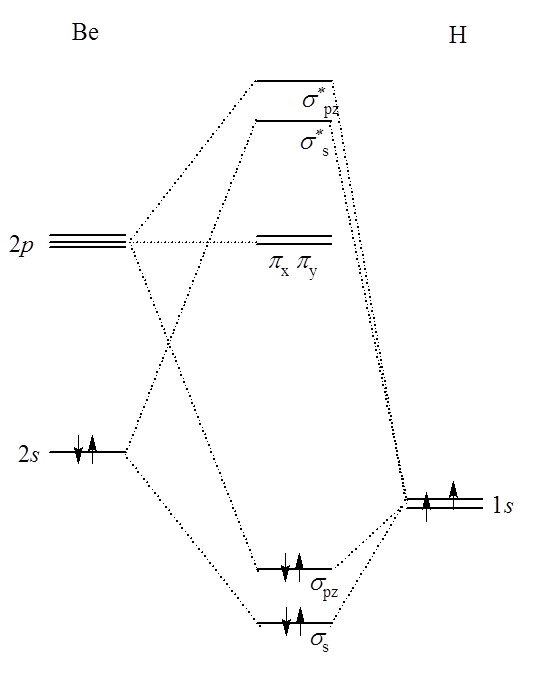
Weźmy pod uwagę dwie cząsteczki trójatomowe – BeH2 i BeF2. Pierwsza z nich jest linową cząsteczką o symetrii D∞h. Przyjmując oś z jako oś symetrii C∞ mamy nakładanie się orbitali atomu Be (2s i 2p) i wodoru. Orbitale px i py nie nakrywają się z orbitalami 1s wodoru ze względu na położenie prostopadłe do osi wiązania i przechodzą w niewiążące orbitale π. Cząsteczka ma środek symetrii, więc orbitale cząsteczkowe będą typu u i g. Orbital σs jest typu g, a σz typu u. Orbitale π są typu u.
 W przypadku fluorku berylu pojawiają się orbitale π.
W przypadku fluorku berylu pojawiają się orbitale π.
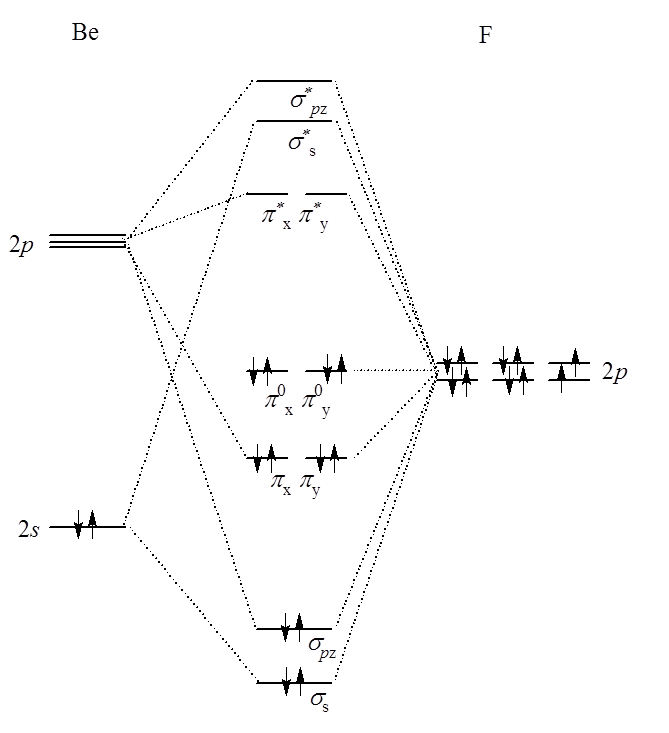
W tym związku orbitale cząsteczkowe σ tworzą się z atomowych orbitali 2s i 2p Be oraz 2pz F. Kombinacja 2px, 2py Be oraz 2px, 2py fluoru tworzy wiązania π. Opisując wiązania w tej cząsteczce rozpatrzyć trzeba nie dwa atomy, a trzy. Tutaj grupa trzech atomów tworzy niepodzielną całość, wokół której rozmyta jest chmura elektronowa tworząca wiązanie; powstaje trójcentrowy orbital cząsteczkowy. Generalnie orbital trójcentrowy może obejmować całą cząsteczkę, i tutaj opis przy użyciu metody orbitali cząsteczkowych jest bardzo adekwatny, lub też stanowić fragment większej całości. W tym drugim przypadku, istotnym dla na przykład borowodorów, metoda orbitali cząsteczkowych nie jest stosowana do rozpatrywania orbitali n-centrowych (gdzie n- oznacza liczbę atomów w cząsteczce) gdyż delokalizacja elektronów nie obejmuje całej cząsteczki, a jedynie jej fragment. Dlatego też uzyskane wyniki dla orbitali n-k centrowych (gdzie k>0) nie różnią się w sposób znaczący od tych jakie uzyskano by rozpatrując całą cząsteczkę.
Zgodnie z diagramem Walsha dla cząsteczek mających cztery lub mniej elektronów walencyjnych korzystna energetycznie jest geometria liniowa. Natomiast kolejne elektrony zajmując orbital πu/a1 powodują zgięcie cząsteczki. Przykładowo cząsteczki NH2 i H2O, zawierające odpowiednio siedem i osiem elektronów walencyjnych nie są liniowe. Uwzględniając efekty wiązania π w cząsteczce związku typu ML2 otrzymujemy diagram Walsha następującej postaci:
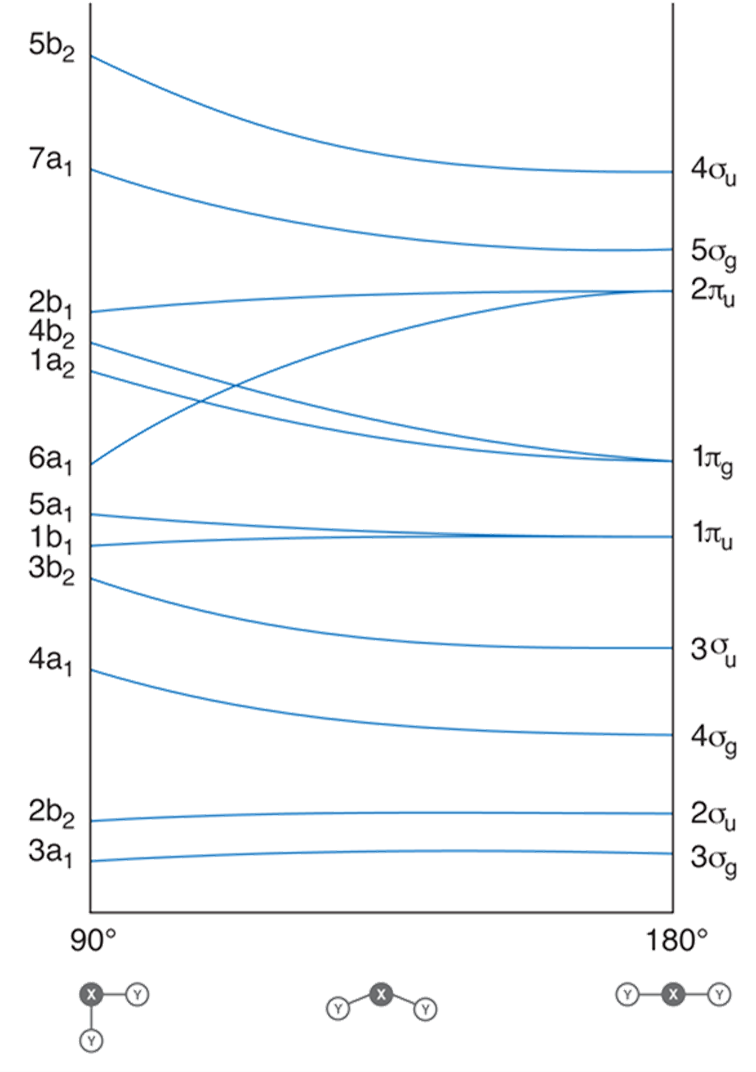 Teraz struktura liniowa lub zgięta jest uzależniona od obsadzenia poziomu 2πu/a1 podobnie jak w przypadku gdy w cząsteczce występowały tylko wiązania σ. Orbitale cząsteczkowe wiążący πu i niewiążący πg mają niższą energię niż antywiążący π*u przez co będą zapełniane jako pierwsze. Cząsteczka będzie liniowa do mementu aż nie osiągnie konfiguracji (σg)2(σg)2(πu)4(πg)4(π*u)1. Od tego momentu korzystniejsze energetycznie będzie zgięcie cząsteczki. Przykładowo cząsteczka NO2 jest zgięta, a mająca jeden elektron mniej cząsteczka CO2 liniowa. W prostych cząsteczka trójatomowych, w których występuje wiązanie π na orbitalach cząsteczkowych można umieścić 12 elektronów bez zginania cząsteczki Do tego dochodzą elektrony tworzące wolne pary elektronowe czyli liczba ta wynosi maksymalnie 15. Cząsteczki o 16 i 17 elektronach będą zgięte podobnie jak cząsteczki o 19 i 20 elektronach walencyjnych gdyż energia orbitalu π*u /b1 prawie nie ulega zmianie podczas zginania cząsteczki. Układy posiadające 21 i 22 elektrony będą liniowe gdyż zapełnione w nich antywiążące orbitale σ* ulegają znacznej destabilizacji podczas zginania cząsteczki.
Teraz struktura liniowa lub zgięta jest uzależniona od obsadzenia poziomu 2πu/a1 podobnie jak w przypadku gdy w cząsteczce występowały tylko wiązania σ. Orbitale cząsteczkowe wiążący πu i niewiążący πg mają niższą energię niż antywiążący π*u przez co będą zapełniane jako pierwsze. Cząsteczka będzie liniowa do mementu aż nie osiągnie konfiguracji (σg)2(σg)2(πu)4(πg)4(π*u)1. Od tego momentu korzystniejsze energetycznie będzie zgięcie cząsteczki. Przykładowo cząsteczka NO2 jest zgięta, a mająca jeden elektron mniej cząsteczka CO2 liniowa. W prostych cząsteczka trójatomowych, w których występuje wiązanie π na orbitalach cząsteczkowych można umieścić 12 elektronów bez zginania cząsteczki Do tego dochodzą elektrony tworzące wolne pary elektronowe czyli liczba ta wynosi maksymalnie 15. Cząsteczki o 16 i 17 elektronach będą zgięte podobnie jak cząsteczki o 19 i 20 elektronach walencyjnych gdyż energia orbitalu π*u /b1 prawie nie ulega zmianie podczas zginania cząsteczki. Układy posiadające 21 i 22 elektrony będą liniowe gdyż zapełnione w nich antywiążące orbitale σ* ulegają znacznej destabilizacji podczas zginania cząsteczki.
Cząsteczki typu ML3
W tego typu cząsteczkach zakładamy istnienie dwóch struktur: płaskiej o symetrii D3h i piramidalnej C3v, w których występują jedynie wiązania σ. Zgodnie z tabelami charakterów orbitale w grupie D3h przekształcają się jak następujące reprezentacje nieprzywiedlne:
| M | s | a’1 |
| M | px, py | e’ |
| M | pz | a”2 |
| 3L | σ | a’1 + e’ |
Orbital pz atomu M jest niewiążący, czyli z orbitalami σ atomów L oddziałują orbitale px, py. W takim wypadku diagram orbitali cząsteczkowych wygląda tak jak na poniższym schemacie:
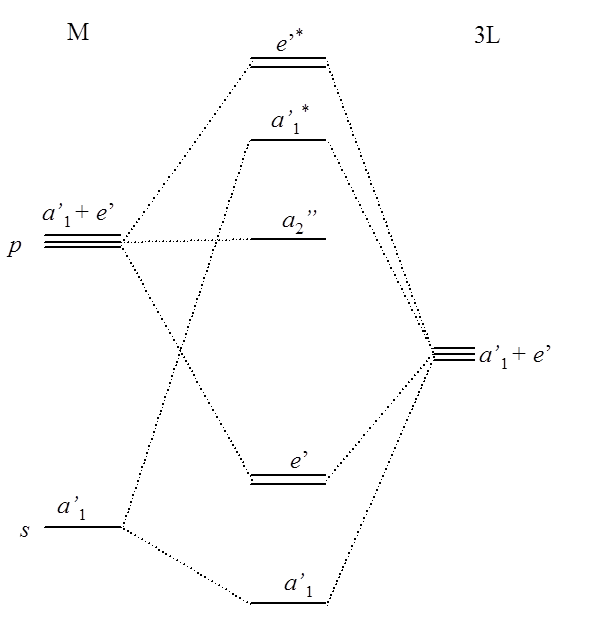 Taka struktura jest trwała w miarę zwiększania liczby elektronów do 6, a jako przykład może służyć płaska cząsteczka BF3. W przypadku geometrii piramidalnej o symetrii C3v orbitale przekształcają się następująco:
Taka struktura jest trwała w miarę zwiększania liczby elektronów do 6, a jako przykład może służyć płaska cząsteczka BF3. W przypadku geometrii piramidalnej o symetrii C3v orbitale przekształcają się następująco:
| M | s | a1 |
| M | px, py | e |
| M | pz | a1 |
| 3L | σ | a1 + e |
W takim wypadku orbital pz nie jest już niewiążący. Diagram orbitali cząsteczkowych jest następujący:
 Oddziaływanie orbitalu pz z orbitalem a1 powoduje obniżenie energii cząsteczkowego orbitalu a1 i podwyższenie energii antywiążącego orbitalu a1*. Geometria piramidalna będzie trwalsza niż płaska jeżeli wiązania w cząsteczce są tworzone przez 8 elektronów. Orbital a1 mający charakter zarówno orbitalu pz jak i s będzie odsunięty od płaszczyzny wyznaczonej przez trzy atomy L Obecność pary elektronowej na tym orbitalu powoduje, że cząsteczki takie są zasadami Lewisa. Jeżeli orbital s atomu M nie uczestniczy w wiązaniu czy to ze względu na kryterium energii czy tez z powodu małej wartości całki nakrywania, to w wiązaniu biorą udział jedynie orbitale p atomu M. W takiej sytuacji katy między wiązaniami są zbliżone do wartości 90°. W przypadku związków o płaskiej geometrii, jak BF3, pusty niewiążący orbital a”2 zlokalizowany na atomie M może przyjąć parę elektronową, czyli cząsteczka zachowuje się jak kawas Lewisa. jednak przyjęcie pary elektronowej zwiększa liczbę elektronów w powłoce walencyjnej i korzystne staje się odkształcenie geometrii cząsteczki z płaskiej do piramidalnej. Można zauważyć, że płaska geometria uwzględniająca tylko orbitale s, i px, py odpowiada hybrydyzacji sp2, a geometrii piramidalnej, angażując orbital s i wszystkie trzy orbitale p – hybrydyzacja sp3.
Oddziaływanie orbitalu pz z orbitalem a1 powoduje obniżenie energii cząsteczkowego orbitalu a1 i podwyższenie energii antywiążącego orbitalu a1*. Geometria piramidalna będzie trwalsza niż płaska jeżeli wiązania w cząsteczce są tworzone przez 8 elektronów. Orbital a1 mający charakter zarówno orbitalu pz jak i s będzie odsunięty od płaszczyzny wyznaczonej przez trzy atomy L Obecność pary elektronowej na tym orbitalu powoduje, że cząsteczki takie są zasadami Lewisa. Jeżeli orbital s atomu M nie uczestniczy w wiązaniu czy to ze względu na kryterium energii czy tez z powodu małej wartości całki nakrywania, to w wiązaniu biorą udział jedynie orbitale p atomu M. W takiej sytuacji katy między wiązaniami są zbliżone do wartości 90°. W przypadku związków o płaskiej geometrii, jak BF3, pusty niewiążący orbital a”2 zlokalizowany na atomie M może przyjąć parę elektronową, czyli cząsteczka zachowuje się jak kawas Lewisa. jednak przyjęcie pary elektronowej zwiększa liczbę elektronów w powłoce walencyjnej i korzystne staje się odkształcenie geometrii cząsteczki z płaskiej do piramidalnej. Można zauważyć, że płaska geometria uwzględniająca tylko orbitale s, i px, py odpowiada hybrydyzacji sp2, a geometrii piramidalnej, angażując orbital s i wszystkie trzy orbitale p – hybrydyzacja sp3.
Cząsteczki o geometrii tetraedru i oktaedru
Weźmy pod uwagę cząsteczki CH4 oraz SF6. Pierwsza jest cząsteczką o symetrii tetraedrycznej (Td), a druga oktaedrycznej (Oh). W przypadku cząsteczki metanu do utworzenia diagramu energetycznego orbitali cząsteczkowych możemy użyć atomowych orbitali 2s22p2 atomu węgla oraz czterech orbitali s1 atomów wodoru rozmieszczonych w przeciwległych narożach sześcianu. Powstawanie pięciocentowych wiążących orbitali cząsteczkowych można przedstawić następującymi schematami:
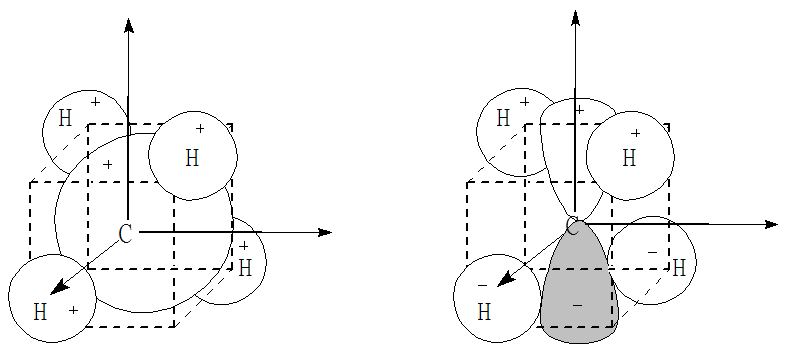 Nakrywanie orbitali 2s i 2p węgla z orbitalami 1s wodoru w cząsteczce metanu.
Nakrywanie orbitali 2s i 2p węgla z orbitalami 1s wodoru w cząsteczce metanu.
Diagram orbitali cząsteczkowych dla metanu jest następujący:
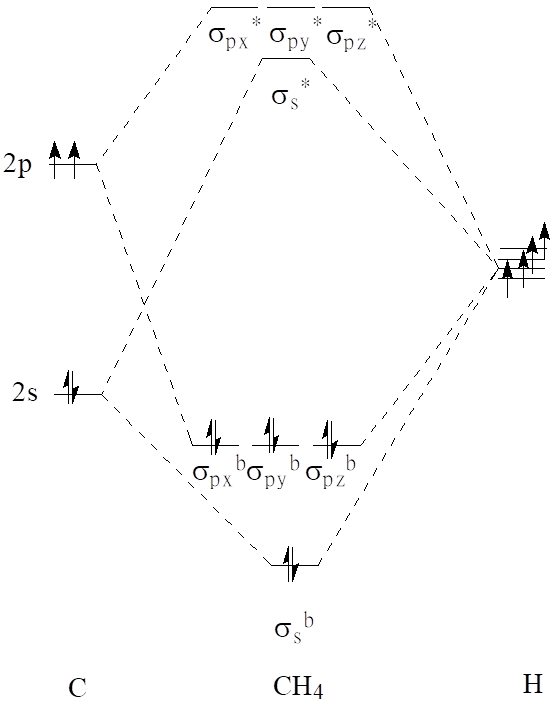
W przypadku cząsteczki SF6 analogicznie umieśćmy atom siarki w środku układu kartezjańskiego, a atomy fluoru w środkach płaszczyzn sześcianu otrzymując okatedryczną cząsteczkę heksafluorku siarki(VI).
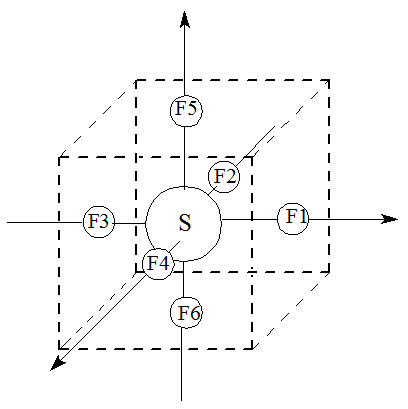
Powłoka walencyjna siarki składa się z orbitali 3s23p63d0, a tworzenie wiązań z atomami fluoru odbywa się poprzez orbitale 2p tego pierwiastka (orbitale 2s F mają za małą energię aby mogły brać udział w tworzeniu orbitali molekularnych). Uwzględniając geometrię oktaedryczną cząsteczki SF6 można łatwo zauważyć, że orbital 3s siarki, jako sferyczny, w wyniku kombinacji z orbitalami p fluoru tworzy orbital cząsteczkowy o symetrii a1g. Orbitale 3p siarki stanowią bazę reprezentacji t w grupie Oh, a że są nieparzyste (zmieniają znak) względem odbicia w środku symetrii powstaje orbital cząsteczkowy t1u w wyniku ich kombinacji z orbitalami p fluoru. Spośród orbitali 3d atomu siarki trzy (dxy, dyz, dxz) przechodzą w niewiążące trójkrotnie zdegenerowane orbitale t2g. Pozostałe dwa, leżące na osiach układu kartezjańskiego, dx2-y2 oraz dz2 tworzą w wyniku kombinacji z orbitalami p fluoru cząsteczkowy orbital eg.
Biorąc pod uwagę powyższe rozważania diagram orbitali cząsteczkowych dla oktaedrycznej cząsteczki SF6 można przedstawić następująco:
