Druga kwantyzacja

Przy opisie układów składających się z dużej ilości jednakowych cząstek stosuje się metodę zwaną druga kwantyzacją. Niech ψ₁(ζ), ψ₂(ζ), ... będzie zupełnym układem unormowanych funkcji falowych tanów stacjonarnych pojedynczej cząstki wybranym tak aby uzyskać dyskretne widmo stanów. W tym celu funkcje falowe dotyczą cząstki o określonej wartości pędu i rzuty spinu oraz rozważa się ruch cząstki w dużym, ale skończonym obszarze przestrzeni Ω. W układzie cząstek pęd każdej z nich z osobna jest zachowany, a tym samym zachowane są liczby obsadzeni stanów, czyli liczby N₁, N₂, ..., wskazujące ile cząstek znajduje się w każdym ze stanów ψ₁, ψ₂, ... . W układzie, w którym cząstki oddziałują ze soba pęd każdej z nich oddzielnie nie jest zachowany, a zatem nie są zachowane liczby obsadzeni stanów. W takim układzie można mówić tylko o prawdopodobieństwie różnych wartości obsadzeni. W takim wypadku należy posłużyć się do opisu układu aparatem matematycznym, w którym liczby obsadzeni a nie współrzędne i rzuty spinów będą odgrywały role zmiennych niezależnych. Stan układu będzie więc opisywany funkcją falową w przestrzeni liczby obsadzeń. Oznaczmy taka funkcję falową przez Φ(N₁, N₂, ...), której kwadrat modułu |Φ|² określa prawdopodobieństwo różnych wartości N₁, N₂, ..., Taki wybór zmiennych niezależnych pociąga za sobą konieczność zdefiniowania operatorów różnych wielkości fizycznych, w tym hamiltonianu, w taki sposób, aby określały ich działanie na funkcje liczby obsadzeń. Sformułowanie tego typu operatorów można uzyskać przez przedstawienie ich w formie macierzowej. Należy przy tym rozważyć elementy macierzowe operatorów działających na funkcje falowe stanów stacjonarnych układu nie oddziałujących ze sobą cząstek. Stany takie można opisać przez podanie określonych wartości liczb obsadzeń, a to prowadzi do możliwości określenia charakteru działania operatorów na te zmienne. 

Statystyka Bosego

Wybierzmy operator pewnej wielkości fizycznej jednej (a–tej) cząstki, czyli taki, który działa tylko na funkcje zmiennych ζ_a i oznaczmy go przez ḟ⁽¹⁾_a. Operator symetryczny względem wszystkich cząstek zdefiniujemy w postaci:

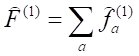i wyznaczymy jego elementy macierzowe względem funkcji falowych. Jak łatwo zauważyć niezerowe będą tylko te elementy macierzowe, które odpowiadają przejściom bez zmiany liczb N₁, N₂, ..., czyli elementy diagonalne, oraz odpowiadające przejściom, w których jedna z tych liczb wzrasta, a druga zmniejsza się o jeden. Wynika to z faktu, że każdy z operatorów ḟ⁽¹⁾_a działa tylko na jedną funkcję z iloczynu ψ₁(ζ), ψ₂(ζ), .., czyli jego elementy macierzowe różne od zera mogą być tylko dla przejść związanych ze zmianą stanu tylko jednej cząstki. Oznacza to, że liczba cząstek znajdujących się w jednym stanie zmniejsza się, a w drugim zwiększa o jedność;

Elementy niediagonalne macierzy operatora są równe:

W równaniu tym element macierzowy f⁽¹⁾_ik oznacza:

Diagonalne elementy macierzowe operatora Ḟ⁽¹⁾ przedstawiają średnie wartości wielkości F⁽¹⁾ w stanach ψ_N1,N2,..., czyli:

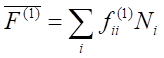 Teraz wprowadźmy operatory â_i działające na nie na funkcje współrzędnych, a na funkcje liczby obsadzeń. Zgodnie z definicją działając na funkcje operator ten zmniejsza o jeden wartość zmiennej N_i i jednocześnie mnoży funkcję przez (N_i)^½:

Ponieważ operator zmniejsza o jeden liczbę cząstek w stanie i-tym nazywany jest operatorem anihilacji. W formie macierzowej:

jedynym elementem niezerowym jest (N_i)^½:

Operator â⁺_i sprzężony z operatorem â_i przedstawia soba na mocy definicji , macierz, której jedynym elementem jest:

Oznacza to, że przy działaniu na funkcję Φ(N₁, N₂, ...) zwiększa o jeden liczbę N_i

i jest nazywany operatorem kreacji cząstek. Iloczyn operatorów kreacji i anihilacji działając na funkcję falową może ją tylko pomnożyć przez pewną stałą nie zmieniając żadnej ze zmiennych N₁, N₂, .... Macierz iloczynu â⁺_i â_i równa jest N_i, a iloczyn â_iâ⁺_i = N_i + 1. W związku z tym reguła komutacji operatorów kreacji i anihilacji jest dana wyrażeniem:

â_iâ⁺_i – â⁺_i â_i = 1

Natomiast operatory o różnych wskaźnikach i, k działając na różne zmienne N_i, N_k , komutują ze sobą:

â_iâ_k – â_k â_i = 0; â_iâ⁺_k – â⁺_k â_i = 0   i ≠ k 

Biorąc pod uwagę właściwości operatorów kreacji i anihilacji można zauważyć, że operator:

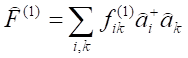jest identyczny z operatorem symetrycznym zdefiniowanym na początku, a jego elementy macierzowe są takie same jak elementy macierzowe początkowego operatora. Wielkości f⁽¹⁾_iik są po prostu liczbami. W ten sposób udało został zdefiniowany operator działający na funkcje liczby obsadzeni. Można go uogólnić na operatory wielkości fizycznych odnoszące się jednocześnie do pary cząstek i działających na funkcje dwóch zmiennych ζ_a, i ζ_b:

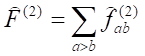Analogicznie można go wyrazić poprzez operatory anihilacji i kreacji:

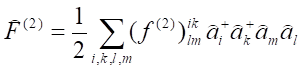gdzie:

W ten sam sposób można uogólnić wzory na operatory symetryczne wszystkich cząstek każdego typu.

Korzystając z przedstawionych wzorów można wyrazić przez operatory kreacji i anihilacji hamiltonian układu złożonego z N wzajemnie oddziałujących jednakowych cząstek, który jest symetryczny względem wszystkich cząstek. Jeżeli oddziaływanie w układzie sprowadza się do wzajemnego oddziaływania każdej pary cząstek, to hamiltonian ma postać:

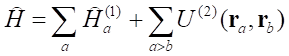Ĥ_a⁽¹⁾ jest częścią hamiltonianu zależną tylko od współrzędnych jednej cząstki, czyli jest to hamiltonian cząstki swobodnej równy:

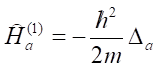Funkcja U⁽²⁾(r₁,r₂) jest energią wzajemnego oddziaływania dwu cząstek. Zastosowanie operatorów kreacji i anihilacji prowadzi do:

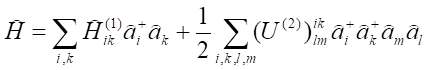 Jest to przedstawienie hamiltonianu w postaci operatora działającego na funkcje liczby obsadzeni.

Dla układu cząstek nie oddziałujących ze sobą w hamiltonianie pozostaje tylko pierwszy człon:

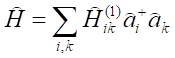Jeżeli jako funkcje ψ_i występują tylko funkcje własne hamiltonianu, to macierz H_ik⁽¹⁾ jest diagonalna, a jej elementami diagonalnymi są wartości własne energii cząstki ε_i, czyli:

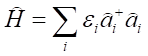Teraz możemy zastąpić operator â⁺_i â_i jego wartościami własnymi i otrzymamy wyrażenie na poziomy energetyczne układu w postaci prostej sumy:

Wzory aparatu matematycznego drugiej kwantyzacji można przedstawić w bardziej zwartej formie stosując operatory:

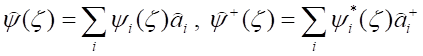gdzie zmienne ζ traktowane są jako parametry. Oczywiście pierwszy z operatorów jest operatorem anihilacji, a drugi kreacji. Ponieważ wyrażenie opisujące te operatory ma analogiczny wygląd jak rozwinięcie funkcji ψ = ∑a_iψ_i na pewien układ zupełny funkcji, czyli jest to jakby ponowne skwantowanie. Stąd właśnie nazwa omawianej metody czyli druga kwantyzacja.

Hamiltonian zapisany za pomocą powyższych operatorów ma postać:

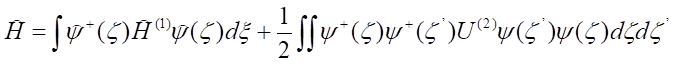Iloczyn operatora kreacji i anihilacji nazywany jest operatorem gęstości cząstek, a całka

pełni rolę operatora całkowitej ilości cząstek w układzie. Jeżeli wstawimy pod całkę wyrażenia na obydwa operatory i uwzględnimy unormowanie oraz wzajemną ortogonalność funkcji falowych otrzymujemy:

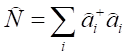Każdy składnik tej sumy jest operatorem ilości cząstek w i-tym stanie, a jego wartości własne są liczbami obsadzeń N_i. Ta statystyka odgrywa szczególną rolę w relatywistycznej mechanice kwantowej.

Statystyka Fermiego

W tym przypadku funkcja falowa ψ_N1N2..., ma teraz postać wyznacznika

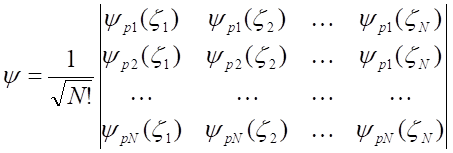analogicznego jak przedstawiony przy omawianiu zagadnienia nierozróżnialności cząstek. Wśród liczb p_i, które numerują cząstki nie może być dwóch jednakowych, gdyż wtedy wyznacznik by znikał. Liczby obsadzeń mogą przyjmować tylko wartości zero i jeden. W związku z antysymetrycznością tej funkcji powstaje problem wyboru jej znaku, który nie występuje w przypadku statystyki Bosego, w której funkcja falowa jest symetryczna. W związku z tym znak funkcji falowej zależy od całego zbioru numerów p_i czyli od wartości wszystkich liczb obsadzeń. W związku z tym i znak operatorów anihilacji i kreacji zależy od tych liczb. Operatory te powinny być określone jako macierze, których jedynym elementem różnym od zera jest:

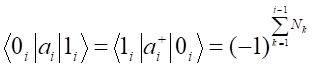Iloczyny macierzy operatorów kreacji i anihilacji są diagonalne, przy czym

a ich suma jest równa

Ponieważ nie można anihilować cząstki w stanie, w której jej niema, jak również nie można kreować cząstki w stanie, w którym występuje inna cząstka (zakaz Paulieg) to iloczyn â⁺_iâ_i znika gdy N_i = 0, a iloczyn â_iâ⁺_i gdy N_i = 1. To oznacza, że

â_iâ_i  = 0,    â⁺_iâ⁺_i  = 0

Dla wszystkich par operatorów o różnych wskaźnikach mamy:

â_iâ_k + â_kâ_i = 0,    â⁺_iâ⁺_k + â⁺_kâ⁺_i = 0,

â_iâ⁺_k + â⁺_kâ_i = 0 dla i ≠ k

czyli wszystkie te operatory antykomutują ze sobą, co oznacza, że przy przestawieniu czynników iloczyn zmienia znak. Wynika to z faktu, że w przypadku statystyki Fermiego wynik działania operatora â_i zależy nie tylko od samej liczby N_i ale również od liczb obsadzeń wszystkich poprzedzających go stanów.Z tego powodu działanie różnych operatorów â_i  i â_k nie można uważać za niezależne.