Równanie Diraca

W nierelatywistycznej mechanice kwantowej funkcje falowe cząstek o różnych spinach są spinorami o różnych rzędach, a funkcje falowe cząstek swobodnych spełniają równanie Schrödingera dla ruchu swobodnego. Cząstkę o spinie zerowym w teorii nierelatywistycznej opisuje skalarna funkcja falowa. W teorii relatywistycznej rolę skalara trójwymiarowego zajmuje skalar czterowymiarowy, niezmienniczy nie tylko względem przekształceń współrzędnych przestrzennych ale również względem transformacji Lorentza. W mechanice relatywistycznej energia cząstki ε i jej pęd p tworzą czterowektor p^μ = (r, p). Odpowiednie operatory są również czterowektorami. Trójwymiarowemu pędowi odpowiada operator równy –i ∇, a energii w równaniu falowym odpowiada operator różniczkowy względem czasu i δ/δt. Dla czteropędu operatorem jest:

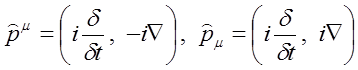Działając na funkcję falową Ψ skalarnym operatorem równym p_μp^μ równym kwadratowi czterowektora pędu. Jak wiadomo kwadrat czteropędu sprowadza się do stałej wielkości czyli kwadratu masy cząstki, a co za tym idzie i wynik jego działania na funkcję falową jest wynikiem jej przemnożenia przez m².n W związku z tym otrzymujemy:

lub w postaci rozwiniętej:

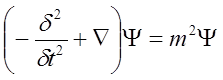Jak widać dla relatywistycznej cząstki o spinie zerowym nie istnieje hamiltonian w takim sensie jak w teorii nierelatywistycznej. Równanie powyższe jest równaniem drugiego rzędu względem czasu, podczas gdy sens hamiltonianu Ĥ polega na tym, że powinien on wyznaczać pierwszą pochodną funkcji falowej zgodnie z równaniem: iδΨ/δt = ĤΨ. Dodatkowo, dla cząstki o spinie zero, kwadrat modułu funkcji falowej nie opisuje gęstości prawdopodobieństwa jej różnych lokalizacji w przestrzeni. Wynika to chociażby z faktu, że gęstość cząstek w teorii relatywistycznej jest składową czasową czterowektora, a nie skalarem. Zatem nie może być określana przez wartość skalarną jaką jest kwadrat |ψ|².

Spinory czterowymiarowe

 W teorii nierelatywistycznej cząstka o spinie s jest opisywana spinorem rzędu 2s, czyli przez 2s + 1 wartości przekształcających się przy obrotach układu współrzędnych według określonych reguł, co wyraża właściwości symetrii cząstki związane z izotropowością przestrzeni. W teorii relatywistycznej obroty przestrzennego układu współrzędnych są jedynie szczególnym przypadkiem obrotów czterowymiarowych. Zbiór wszystkich możliwych przekształceń nosi nazwę grupy Lorentza. Oprócz obrotów w przestrzeni trójwymiarowej dochodzą tutaj przekształcenia Lorentza, czyli obroty w jednej z płaszczyzn xt, yt, zt. W związku z tym opis cząstek posiadających spin wymaga teorii spinorów czterowymiarowych, odgrywających taką sama rolę jak trójwymiarowe spinory względem grupy obrotów w przestrzeni. Czterospinory pierwszego rzędu

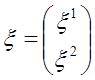mają dwie składowe, które przy dowolnym przekształceniu Lorentza transformują się jak:

ξ^1’ = αξ¹ + βξ;²

ξ^2’ = γξ¹ + δξ²

gdzie zespolone współczynniki α, β, γ, δ są określonymi funkcjami obrotów czasoprzestrzennego układu współrzędnych. W ogólnym przypadku obroty te odbywają się wokół sześciu kątów w sześciu płaszczyznach: xy, xz, yz, tx, ty, tz. ξ^1’i ξ^2’ dla cząstki o spinie połówkowym odpowiadają wartościom własnym rzuty spinu na oś z, równym +½ i –½. Podobnie jak dla spinorów  trójwymiarowych, współczynniki przekształcenia związane są równością:

αδ – γβ = 1

Zależność ta prowadzi do tego, że antysymetryczna kombinacja liniowa składowych dowolnych dwu spinorów

ξ¹Ξ¹ + Ξ¹ξ¹

jest niezmiennicza, co określa regułę tworzenia iloczynu skalarnego dwu spinorów. Natomiast gdy rozpatrzymy spinory sprzężone w sposób zespolony, to w przypadku spinorów trójwymiarowych reguła transformacji:

 ξ¹ξ^1* + ξ²ξ^2*

określała gęstość prawdopodobieństwa znalezienia cząstki w przestrzeni i prowadziła do zależności pomiędzy współczynnikami α, β, γ, δ. W teorii relatywistycznej gęstość cząstek nie jest skalarem, a w związku z tym nie może określać prawdopodobieństwa i nie nakłada żadnych dodatkowych warunków ma współczynniki przekształcenia. Tutaj cztery wielkości zespolone są, czyli mamy sześć parametrów rzeczywistych związane tylko jednym warunkiem co odpowiada liczbie parametrów przekształceń grupy  Lorentza. W takim razie przekształcenie

ξ^1’ = αξ¹ + βξ;²

ξ^2’ = γξ¹ + δξ²

i przekształcenie sprzężone z nim w sposób zespolony są różnymi przekształceniami., co oznacza, że w teorii relatywistycznej występują dwa typy spinorów. Kolejnym elementem jaki nie występował w teorii nierelatywistycznej jest zagadnienie inwersji spinorów. Spinory trójwymiarowe względem operacji inwersji nie ulegają zmianie. Inaczej sytuacja wygląda w przypadku spinorów czterowymiarowych. Inwersja polega na zmianie kierunku osi x, y, z układu współrzędnych na przeciwny. Dwukrotne przeprowadzenie inwersji doprowadza układ do stanu początkowego, jednak w przypadku spinorów powrót do stanu wyjściowego można rozumieć dwojako. W jednym przypadku będzie to obrót układu współrzędnych o kąt 0°, a w drugim o kat 360°. Te dwa obroty nie są równoważne gdyż spinor czterowymiarowy przy obrocie o kat 360° zmienia znak. W związku z tym istnieją dwie alternatywne koncepcje inwersji spinorów, zgodnie z którymi dwukrotna inwersja albo nie powinna zmieniać znaku, albo znak spinora powinien ulegać zmianie. Wybór którejkolwiek z nich nie ma wpływu na fizyczne wyniki, w związku z czym wybierzmy do rozważań tę wersję przy której znak spinora nie ulega zmianie. Inwersja współrzędnych zmienia znak wektorów biegunowych ale nie zmienia znaku wektorów osiowych. Do wektorów osiowych należy wektor momentu pędu, czyli również spinu, zatem nie zmienia się przy inwersji wartość rzutu spinu na oś z. Z tego wynika, że przy inwersji każda ze składowych ψ¹ i ψ² spinora trójwymiarowego, odpowiadających określonej wartości s_z, może przekształcać się tylko na siebie. W przypadku spinorów czterowymiarowych taka zależność nie może mieć miejsca. Natomiast dołączenie inwersji do liczby dopuszczalnych przekształceń spinorów czterowymiarowych wymaga jednoczesnego rozważania par spinorów, z których jeden ma inne właściwości transformacyjne niż dany spinor.

Weźmy pod uwagę cząstkę o spinie ½, której funkcja falowa w teorii relatywistycznej jest bispinorem, czyli ma cztery składniki zamiast dwóch jak w teorii nierelatywistycznej. Pod działaniem operatora p_μp^μ zostaje ona pomnożona przez m², przy czym nie rozwiązuje to problemu znalezienia równania falowego dla takiej cząstki. Z czterech składowych bispinorowych funkcji falowych tylko dwie mogą być liniowo niezależne, co wynika z liczby wartości, które może przyjmować rzut spinu połówkowego. W związku z tym pełny układ równań falowych powinien być liniowym układem różniczkowym między składowymi bispinora, otrzymanym za pomocą operatora p_μ = iδ/δx^μ i układ ten powinien być relatywistycznie niezmienniczy. Dla swobodnej cząstki poruszającej się z określonym pędem p i energią ε wszystkie składowe funkcji falowej są proporcjonalne do czynnika e^{i(pr – εt)}. W wyniku działania operatora pędu funkcja zostaje pomnożona przez ε, a w wyniku działania operatora pędu jest mnożona przez wektor p. W rezultacie układ równań różniczkowych sprowadza się do układu równań liniowych składającego się z dwóch par. Każda z par tych równań określa dwie składowe bispinora, gdy dane są dwie inne składowe. Aby układ równań nie był sprzeczny musi zachodzić:

ε² – p_x² – p_y² – p_z² = ε² – p² = m²

co jest relatywistycznym przedstawieniem wyrażenia na energię cząstki przez jej pęd. Ponieważ z czterech składowych bispinorowej funkcji falowej swobodnej cząstki, tylko dwie mogą być dowolne, to odpowiada to fizycznie temu, że przy zadanym pędzie stany cząstki mogą różnić się rzutem spinu przyjmującym tylko dwie wartości.

Macierze Diraca

Czteroskładnikową funkcję (bispinor) falową możemy zapisać w postaci kolumny:

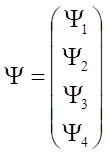a układ równań Diraca w postaci:

gdzie γ^μ (μ = 0, 1, 2, 3) są pewnymi macierzami czwartego rzędu o elementach γ^μ_ik (i, k = 1, 2, 3, 4). Dla spinorowej reprezentacji funkcji falowej macierze te przyjmują postać:

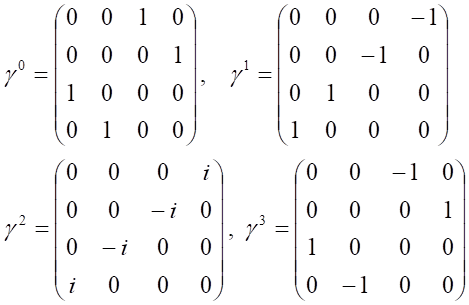Macierze γ^μ noszą nazwę macierzy Diraca. Zapisując równanie Diraca w postaci rozwiniętej względem pochodnej po czasie, dla cząstek o spinie ½, można zdefiniować hamiltonian. Przemnożenie równania:

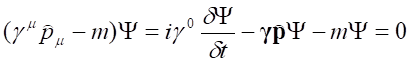przez γ⁰ powoduje, że współczynnik przy δψ/δt przyjmuje wartość jednostkową (macierz jednostkowa) i otrzymujemy zależność:

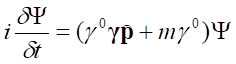 W ten sposób operator działający na ψ po prawej stronie równania jest hamiltonianem cząstki.